Técnicas Matemáticas de Resolución de Problemas

Funciones elementales reales

Función potencia.

Función potencia de base real y exponente natural.

Dado un número natural n se define la potencia n-ésima de un número real x como el producto de n factores iguales a x:

xⁿ=x.x. ... ⁿ⁾.x

Dado un número natural n se define la función potencia n-ésima como la función real de variable real que a cada x le asigna xⁿ.

El cálculo con potencias tiene las siguientes propiedades:

         1   (xy)ⁿ =xⁿ yⁿ cualesquiera que sean x,yÎ IR.
         2   xⁿ x^m =x^n+m  con xÎ IR.
         3   (xⁿ) ^m =x^{n m} con xÎ IR.
           4    Si  0<x<y  entonces  0< xⁿ <yⁿ. Como consecuencia de esta propiedad se tiene

 5    La función potencia n-ésima no está acotada superiormente, es decir

 6 La función potencia n-ésima es una función continua en IR

.

7   La función potencia n-ésima tiene derivadas continuas de cualquier orden:

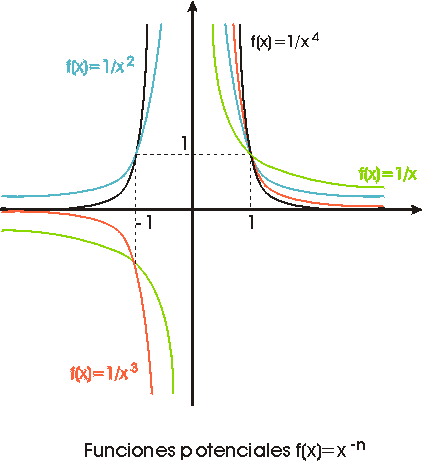
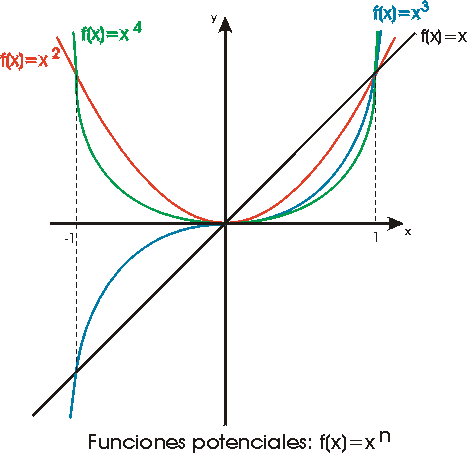
La siguiente figura muestra la gráfica de varias funciones potenciales de exponente natural
 
 

 

 

 

Funciones polinómicas y racionales

Una función polinómica es una combinación lineal de funciones potencias de base real y exponente natural:

Las funciones polinómicas son continuas e indefinidamente derivables en todo IR.
 

 
 

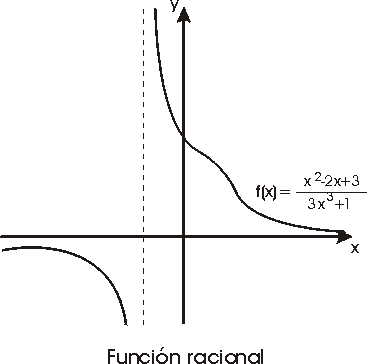
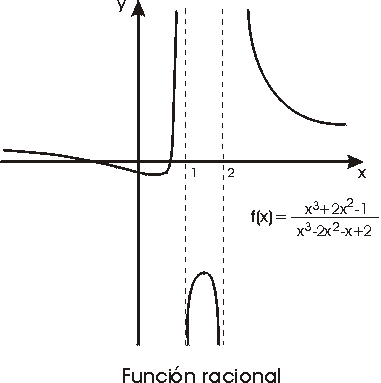
Una función racional es una función que se obtiene como cociente de dos funciones polinómicas:

 

Una función racional está definida en todo los números reales excepto en los puntos donde el denominador se anula. En su dominio de definición, las funciones racionales son continuas e indefinidamente derivables.
 
 
 

 
 
 
Potencias de base real y exponente entero.

Cuando el exponente es un entero positivo recuperamos la definición del apartado anterior.
Para los enteros negativos -n  se define

                                            x^-n=(1/x)ⁿ=(x^-1)ⁿ

y finalmente  si n=0 convendremos que x⁰=1. Tenemos pues

Para cualquier número entero n se define la función potencia n-ésima como la función que a cada x le asigna xⁿ.

Las propiedades 1, 2 y 3 que vimos para las potencias de exponente natural se generalizan sin dificultad a este caso. Para exponente negativo –n tenemos:

4’ Si 0<x<y entonces 0<y^-n<x^-n. Es decir la potencia de exponente negativo es una función estrictamente decreciente en (0,¥ ).

5’ La función potencia de exponente negativo esta acotada inferiormente en (0,¥ ). Más concretamente se tiene

6’ Sin embargo, no está acotada superiormente en dicho intervalo puesto que

Las siguientes gráficas muestran algunas funciones potencia con exponente negativo; nótese que en el 0 no están definidas.

 

Raíces de índice natural de números reales positivos.

Dado un número real positivo x y un número natural n, se dice que otro número real y es la raíz n-ésima de x si se verifica yⁿ=x.

• Todo número real positivo posee una única raíz n-ésima positiva.
• Si n es par  los  números reales positivos tienen además una raíz n-ésima negativa.

 

En la figura se muestran las gráficas de las funciones raiz segunda, tercera y cuarta positivas.