Técnicas Matemáticas de Resolución de Problemas

Secciones Cónicas

Estas curvas aparecían ya en la geometría griega y fueron denominadas secciones cónicas, ya que los griegos de la época de Platón consideraban que tales curvas procedían de la intersección de un cono con un plano.

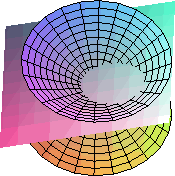
    Las elipses son las curvas que se obtiene cortando una superficie cónica con un plano que no es paralelo a ninguna de sus generatrices.

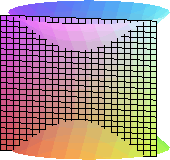
    Las hipérbolas son las curvas que se obtiene al cortar una superficie cónica con un plano que es paralelo a dos de sus generatrices (Base y arista).

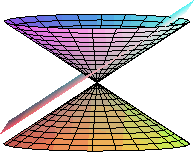
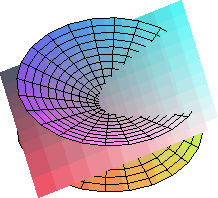
    Las parábolas son las curvas que se obtienen al cortar una superficie cónica con un plano paralelo a una sola generatriz (Arista).

La Elipse como sección cónica

La Hipérbola como sección cónica

La Parábola como sección cónica

Cuando los matemáticos de los siglos XVI y XVII estudiaron los trabajos griegos, empezaron a comprobar la falta de generalidad de los métodos de demostración lo que llevo a sustituir la visión puramente geométrica de las secciones cónicas por otra que incorporaba las nociones de coordenadas y distancia. Esto llevo a la definición de estas curvas como lugares geométricos de puntos que verificaban ciertas propiedades en términos de distancia.

La ecuación de una cónica puede simplificarse girando y trasladando los ejes coordenados de forma que sólo queden los términos elevados al cuadrado y el término independiente. Esta forma de la ecuación se llama ecuación reducida o canónica de la cónica.

Haciendo los cambios oportunos la ecuación general se puede transformar en una de los siguientes:

Elipse
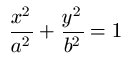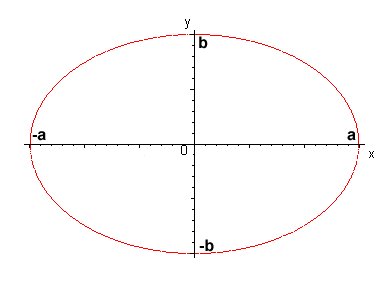Circunferencia (Caso particular de la elipse)
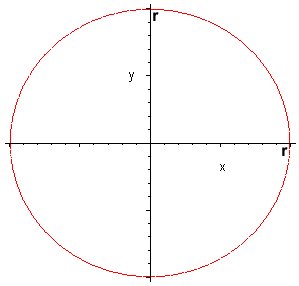Hipérbola
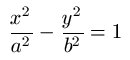Parábola
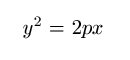
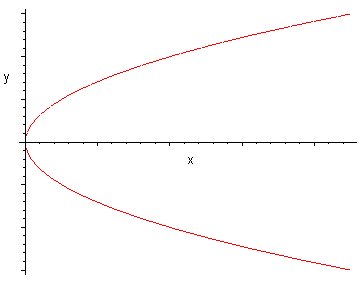
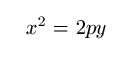
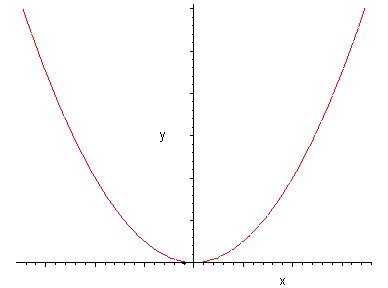