Técnicas Matemáticas de Resolución de Problemas

Derivada de una función

El concepto de derivada lo podemos encontrar en la actualidad en prácticamente cualquier ciencia. La derivada, junto con la práctica totalidad del cálculo infinitesimal básico, fue inventada prácticamente al mismo tiempo aunque de manera independiente por Newton y Leibnitz. Definición de la derivada Sea una función f(x) y consideremos la siguiente fracción: Esta fracción, además del significado geométrico que veremos en seguida, se puede interpretar como "lo que crece la función por unidad de x", o la rapidez de crecimiento de la función a lo largo del eje x. El lector que tenga problemas para visualizar esto podrá verlo con facilidad si sustituye funciones concretas, por ejemplo en lugar de f(x) se puede utilizar s(t) (la función que dice el camino recorrido por un cuerpo en el instante t), y en lugar de x la propia variable t. Con esta sustitución, la fracción quedaría como que es precisamente la velocidad media del cuerpo en el intervalo Δt. 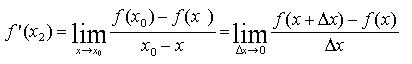Pues bien, se define la derivada de la  función f(x) en el punto x2 [se escribe f'(x2) - con un apóstrofe siguiendo al nombre de la función] como el límite Intuitivamente, esto significa que vamos reduciendo cada vez más el intervalo en el que efectuamos el promedio de crecimiento de la función, hasta el punto de dejar reducido ese intervalo a un punto. La derivada representa, pues, el crecimiento instantáneo de una función en un punto. Es importante señalar que nada obliga a que este límite exista, pero si existe, se dice que la función es derivable en el punto x0. 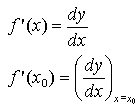En muchas ocasiones veremos la derivada expresada de las siguientes formas:   donde dy y dx  se llaman infinitésimos, y se asumen infinitamente pequeños. Tanto dy como dx  son un único símbolo, es decir, no podemos "cancelar" la parte "d" del numerador y denominador para que solamente quede y/x. 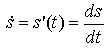Cuando la función que se está derivando es una función que depende del tiempo, se ha extendido indicar la derivada con un punto encima de la función: Significado geométrico Para entender el significado geométrico de la derivada, volvamos a nuestra fracción original y representemos los valores sobre el gráfico de la función. 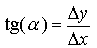En rojo hemos indicado los puntos x0 y x, respectivamente Por el triángulo rectángulo que tenemos podemos decir que   Veamos ahora lo que ocurre cuando hacemos tender Δx a cero, lo cual básicamente significa que el punto x se va acercando al x0 Siguiendo con este proceso, podemos ver como en el momento que se "juntan" los dos puntos (es decir, en el límite) la recta que cortaba la curva se convierte en una tangente a la curva en ese punto, y por lo tanto el valor de la fracción se convierte en la tangente del ángulo.   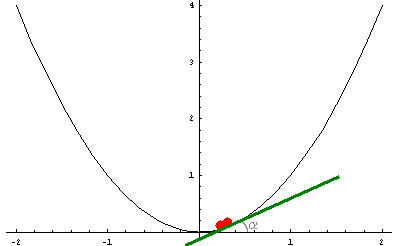Así pues, la derivada de una función en un punto es el valor de la tangente del ángulo que la recta tangente a la curva en se punto forma con el eje de las abcisas.