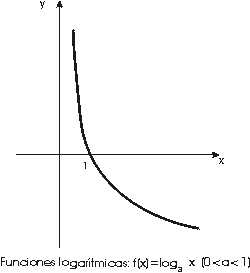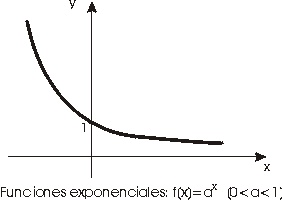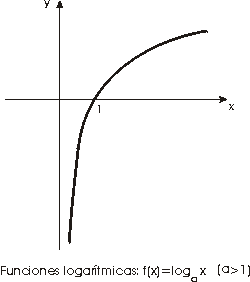Técnicas Matemáticas de Resolución de Problemas

Funciones elementales reales

La función exponencial

Sea a un número real positivo. La aplicación que a cada número real x le asigna la potencia a^x se denomina función exponencial de base a.

Las figuras siguientes muestran funciones exponenciales en las que se observan las propiedades que se detallan a continuación.
 
 

 
 
  Propiedades:

• a^x >0 para todo xÎ IR .
• La función exponencial de base a>1 es estrictamente creciente, mientras que la de base a<1 es estrictamente decreciente.
• La función exponencial de base mayor que 1 no está acotada superiormente aunque si lo está inferiormente IR.
• Se tiene
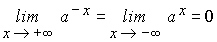
• Si  0<a<1 la función exponencial de base a no está acotada superiormente aunque si lo esta inferiormente en IR. De hecho se verifica:
  
   
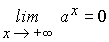
• Si  0<a<b  entonces:   a^x < b^x  si x>0     y  b^x < a^x  si  x<0.
• Cualquiera que sea el número real positivo y existe un único número real x tal que a^x=y. El número x se llama logaritmo en base a de y y se representa
  

Esta última propiedad nos sirve para definir una nueva función, inversa de la anterior en el sentido de que la composición de ambas da la función identidad.
 

La función logarítmica

Sea a un número real positivo. La aplicación que a cada número real x>0 le asigna log_a x (que es único) se denomina función logarítmica en base a.

Las propiedades de está función se deducen inmediatamente de las de la función exponencial:

• log_a (xy)=log_a x+log_ay   para cualesquiera  x,yÎ IR.
• Si a>1 la función logaritmo correspondiente es estrictamente creciente, y si 0<a<1 entonces es estrictamente decreciente en (0,+¥ ).
• Para base a>1 la función logarítmica no esta acotada superior ni inferiormente. De hecho se tiene
  
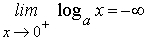
• Para base 0<a<1 la función logarítmica no esta acotada superior ni inferiormente y se tiene
  
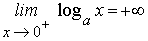
• Para todo número real  x>0  se tiene  log_a x=log_bx log_a b,  cualesquiera que sean los números reales positivos a y b