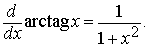Técnicas Matemáticas de Resolución de Problemas
Funciones elementales reales
Las funciones trigonométricas.
Las funciones trigonométricas básicas son el seno y el coseno. El resto de las funciones trigonométricas se obtiene a partir de ellas. Comenzamos con una definición informal.
Un ángulo dirigido puede ser considerado como un par de semirrectas (l1,l2) con el mismo punto inicial.
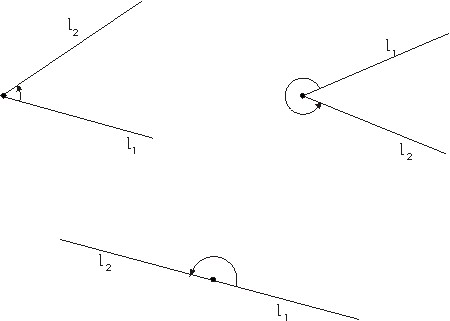
Si para l1 elegimos siempre la mitad positiva del eje horizontal, un ángulo dirigido vendrá descrito mediante la segunda semirrecta. Puesto que cada semirrecta corta al círculo unidad exactamente una vez, un ángulo dirigido queda descrito, aún más sencillamente, mediante un punto sobre el círculo unidad, es decir un punto (x,y) tal que x2+y2=1.

Entonces el seno del ángulo se define como la ordenada y del punto que lo representa y el coseno como la abcisa x, según se representa en la figura siguiente:
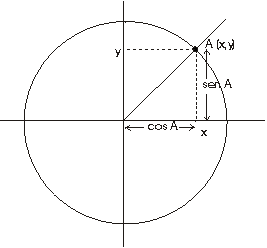
Sin embargo queremos definir el seno y el coseno de cualquier número real x .
El procedimiento usual es asociar un ángulo a cada número.
Esta asociación se lleva a cabo del modo siguiente: dado un número real cualquiera x, elíjase un punto P sobre el círculo unidad tal que x sea la longitud del arco de círculo que empieza en (1,0) y que se dirige hacia P en sentido contrario al de las agujas de un reloj.
El ángulo así construido determinado por P se denomina ángulo de x radianes. Al ser 2p la longitud total del círculo, el ángulo de x radianes y el ángulo de 2p +x radianes son idénticos.Se puede definir ahora el seno de x como el seno del ángulo de x radianes.
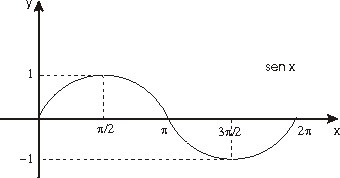
Esta definición se extiende primero al intervalo [-p , 0 ) de la forma siguiente:
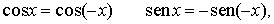
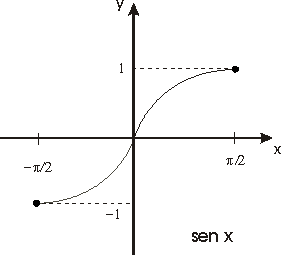
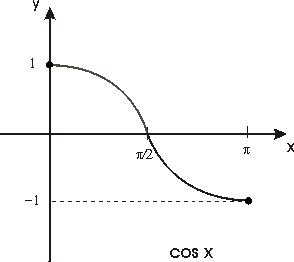
Por último, la definición de las funciones seno y coseno se extiende a toda la recta real de forma periódica.
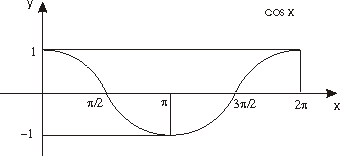
Las figuras siguientes muestran esta extensión.


Las funciones seno y coseno son continuas en IR y admiten derivada en todo punto verificándose que
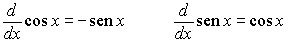
Además, son funciones acotadas puesto que verifican las siguientes igualdades:
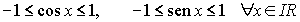
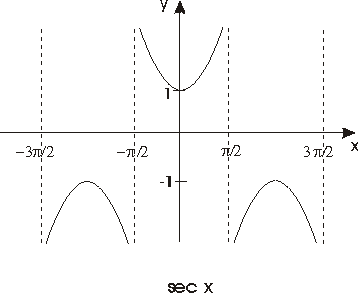
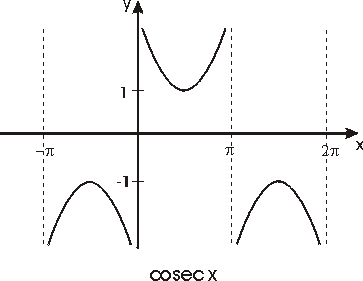
El resto de las funciones trigonométricas se definen como sigue:
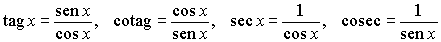
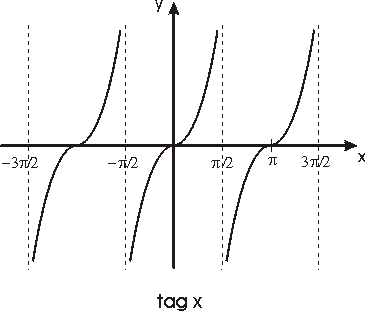
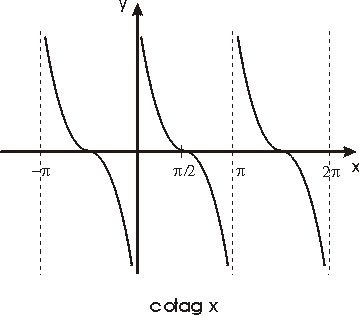
Véanse las gráficas de estas funciones en las figuras siguientes
Propiedades de las funciones trigonométricas.
cos2 x + sen2 x =1,
cos(x+y)=cos x cos y - sen x sen y, cos 2x= cos2 x - sen2x
cos(x- y)= cos x cos y + sen x sen y,
sen (x+y)=sen x cos y + cos x sen y, sen 2x= 2cos x sen y
sen (x- y)=sen x cos y- cos x sen y
Las funciones trigonométricas inversas.
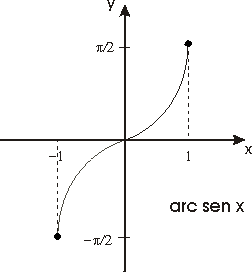
La función f(x)=sen x, definida en el intervalo cerrado [-p /2,p /2], es continua, estrictamente creciente y transforma dicho intervalo en el [-1, 1]. A su función inversa la denotaremos por
f -1(x)=arc sen x
estará definida de [-1, 1] siendo también continua y estrictamente creciente.
Es inmediato comprobar que arc sen (- x)=- arc sen x para todo x en [-1, 1].
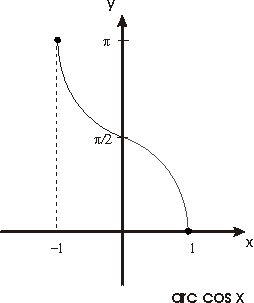
La función f(x)=cos x, definida en el intervalo cerrado [0, p ], es continua, estrictamente decreciente y transforma dicho intervalo en el [-1, 1]. Esta función es pues un homeomorfismo del primer intervalo sobre el segundo y su función inversa que denotaremos por
f -1(x)=arc cos x
estará definida de [-1, 1] siendo también continua y estrictamente decreciente.
Las funciones trigonométricas inversas arc cos x y arc sen x definidas en el intervalo [-1,1] son derivables en todos los puntos de (-1, 1) y se tiene
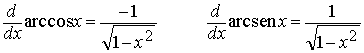
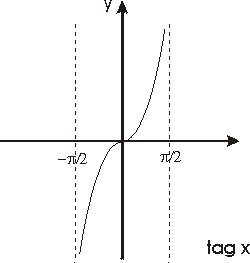
La función f(x)=tag x, definida en el intervalo (-p /2,p /2), es continua, estrictamente creciente y transforma dicho intervalo en IR puesto que
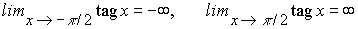
Esta función es pues un homeomorfismo del primer intervalo sobre toda la recta real y su función inversa
f -1(x)=arc tag x
que estará definida en IR, es también continua y estrictamente creciente.
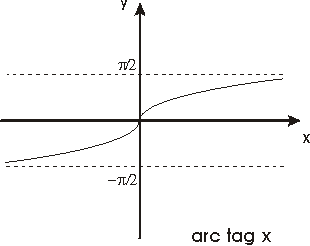
Además arc tag x es derivable en todo punto y su derivada viene dada por