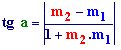Técnicas Matemáticas de Resolución de Problemas

Coordenadas Cartesianas

La idea básica es representar la posición de un punto en el plano o en el espacio.

Fue Descartes el primero que utilizó el método de las coordenadas para indicar la posición de un punto (en el plano o en el espacio), por eso se suele decir coordenadas cartesianas. Descartes utilizó, para representar un punto en el plano, dos rectas perpendiculares entre sí. La posición del punto se lograba midiendo sobre los ejes las distancias al punto, de la manera que se puede ver en el dibujo.

    El sistema de coordenadas cartesianas es una manera de identificar la posición de un punto sobre un plano en relación a estas rectas perpendiculares llamados ejes. El eje horizontal también se llama eje de X o, de abcisas y el eje vertical se llama eje de Y o de ordenadas. El punto de intersección de los ejes se llama origen de coordenadas. Sobre cada recta se establece una recta numérica de manera que el valor 0 corresponde al punto origen, los valores positivos corresponden a los puntos a la derecha del eje X o hacia arriba del eje Y, y los valores negativos corresponden a los puntos a la izquierda del eje X o hacia abajo del eje Y.

    Las coordenadas de un punto es un par ordenado (x,y) que identifica la posición que este se encuentra con respecto a los ejes. La primera coordenada (x) o abscisa es la posición del punto con respecto al eje horizontal o eje de x. La segunda coordenada u ordenada es la posición del punto con respecto al eje vertical o eje de y.

El sistema de coordenadas cartesianas divide el plano en cuadro regiones llamaos cuadrantes. Los cuadrantes nos ayuda a identificar rápidamente la posición de un punto:

Vectores

Dos puntos del plano A y B, determinan un vector con origen A y extremo B que es donde se encuentra la punta de la flecha.

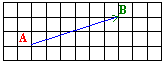
El módulo de un vector a es la longitud del vector y se expresa con la misma letra entre barras.

Módulo del vector a = |a|

La dirección del vector es la dirección de la recta donde se encuentra y la de todas sus paralelas. Por ejemplo los vectores x e y tienen la misma dirección.

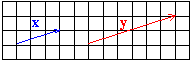
El sentido de un vector lo indica la punta de la flecha. Por ejemplo los vectores x e y de la figura anterior tienen el mismo sentido.

Dos vectores son iguales si tienen el mismo módulo, la misma dirección y el mismo sentido.

Dos vectores iguales x e y situados en rectas distintas determinan un paralelogramo.

Ecuaciones de la recta
 
Una recta r queda determinada vectorialmente del siguiente modo:

  • Dando un punto P de la recta.
  • Dando un vector, d, paralelo a la recta llamado vector dirección

    • En general, p+td es un vector que, si se sitúa con su origen en O, tiene su extremo, X, sobre la recta r y se desliza sobre ella al variar t.

    ECUACIÓN VECTORIAL DE LA RECTA

    Ésta que se ha descrito es la ecuación vectorial de la recta:

    OX = p + td
    O es el origen de coordenadas 
    X es un punto cualquiera variable de la recta 
    p es el vector posición de un punto P conocido de la recta 
    d es un vector dirección conocido, paralelo a la recta 
    t es un parámetro. Al dar valores a t, obtendremos los distintos puntos X de la recta

    ECUACIONES PARAMÉTRICAS DE LA RECTA

    Si en la ecuación vectorial se sutituyen los vectores por sus coordenadas, queda así:

    (x,y) = (p1,p2) + t (d1,d2)

    Expresando por separado cada coordenada se obtienen las ecuaciones paramétricas:

    (x,y) son las coordenadas de un punto cualquiera desconocido de la recta 
    (p1,p2) son las coordenadas de un punto conocido de la recta 
    (d1,d2) son las coordenadas de un vector paralelo a la recta 
    t es un parámetro. Para cada valor que le demos a t se obtiene un punto (x,y) de la recta

    ECUACIÓN GENERAL O IMPLÍCITA DE LA RECTA

    Si en las ecuaciones paramétricas eliminamos el parámetro (por ejemplo, despejando t en una de ellas y sustituyendo su valor en la otra), se obtiene una única ecuación del tipo:  

    Ax + By + C = 0

    Ecuación explícita de la recta. Pendiente

        Si en la ecuación implícita Ax + By + C = 0 es B distinto de 0, podemos despejar la y, obteniendo una ecuación de la forma:
     

    y = mx + n Ecuación explícita de la recta m es la pendiente de la recta   
    n es la ordenada en el origen

        La pendiente de una recta es el incremento de la ordenada (y), cuando la abcisa (x) se incrementa en una unidad. Es fácil ver también, que la pendiente de una recta es la tangente trigonométrica del ángulo a que forma la recta con la parte positiva del eje X.

    La pendiente de la recta que pasa por P1(x1,y1) y P2(x2,y2) es:

    Vector normal a una recta 

    Se llama vector normal a una recta a cualquier vector perpendicular a ella.
    Recta en paramétricas

    		El vector (d,-b) es normal a r, pues es perpendicular a su vector dirección (b,d): 

    (d,-b).(b,d) = db-bd = 0
    Recta en implícita Ax + By + C = 0 El vector (A,B) es normal a r

    Ángulo entre dos rectas

    Se llama ángulo entre dos rectas al menor de los ángulos que forman éstas. 
    El ángulo, A, entre dos rectas r1 y r2, se puede obtener a partir de sus vectores dirección, d1, d2, o a partir de sus vectores normales, n1, n2:

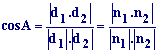    Paralelismo y perpendicularidad de rectas
     

    Si (d1, d2) es un vector dirección de r, entonces:
    Cualquier recta con vector dirección (d1, d2) o proporcional a él, (kd1, kd2), k distinto de 0, es paralela a r o coincide con r
    Cualquier recta con vector dirección (d2, -d1) o proporcional a él, (kd2, -kd1), k distinto de 0, es perpendicular a r

    Relación entre las pendientes m1 y m2 de dos rectas r1 y r2

    rectas

    r1: y = m1x + n1

    r2: y = m2x + n2

    ángulo entre ambas= a

    Son paralelas si

    a = 0º

    m1 = m2

    Son perpendiculares si

    a = 90º

    1 + m1.m2 = 0

    m1.m2 = -1

    Posición relativa de dos rectas 

    Dadas las rectas r1:  r2: 

    		 para hallar su posición relativa, resolvemos el siguiente sistema de ecuaciones con dos incógnitas, t y s:

    		Igualamos la x y la y de las dos rectas utilizando parámetros distintos, t y s, para una y otra.
    Si el sistema tiene solución única (t0,s0), las rectas se cortan en un punto, cuyas coordenadas se obtienen sustituyendo, en r1, t por t0, o bien, en r2, t por s0
    Si el sistema no tiene solución, las rectas son paralelas.
    Si el sistema tiene infinitas soluciones, son la misma recta.

    Posición relativa de rectas dadas en forma general
     

    Sistema con las rectas

    Solución única Se cortan en 1 punto

    No tiene solución Paralelas

    Infinitas soluciones Son la misma recta

    Distancia entre dos puntos

    Distancia entre dos puntos P(x1,y1), Q(x2,y2) es el módulo del vector PQ 
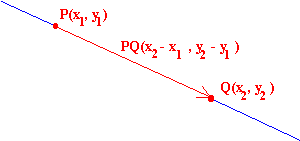    dist(P,Q) = |PQ| = 

    Distancia de un punto a una recta  

    La distancia del punto P(a,b) a la recta r:Ax + By + C = 0 es: dist(P,r) =