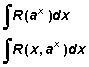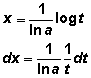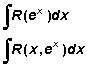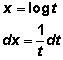|
Este método consiste en transformar la integral dada en otra más
sencilla mediante un cambio de la variable independiente. Aunque
algunos casos tienen un método preciso, es la práctica, en general,
la que proporciona la elección del cambio de variable más
conveniente.
Se comenzará por estudiar aquellas integrales que son casi
inmediatas.
Si en lugar de x se tuviese una función u(x),
la regla de la cadena
Por tanto,
Como se ve, se ha escrito u en lugar de u(x) por
simplificar la notación. |