Ecuación del calor
Resumen: En este ejemplo vamos a considerar un problema parabólico dependiente de tiempo.
Problema considerado
Sean
Se trata de la ecuación del calor en la que la variable
Para calcular una solución aproximada del problema
Discretizamos en tiempo tratando la variable
Cada problema estacionario se resuelve mediante el método de los elementos finitos sobre una triangulación dada, como en los ejemplos anteriormente considerados.
Distretización en tiempo
Consideramos una partición uniforme del intervalo
Para
Para cada
Pongamos
Sustituyendo la derivara de
Teniendo en cuenta esta expresión en la ecuación diferencial de
Para cada
Por tanto, el esquema discreto en tiempo es como sigue: dado
Obsérvese que, para cada
Discretización en espacio
Formulación variacional
Observación: todos los cálculos que se hacen en esta sección son puramente formales, es decir, se supone siempre la regularidad suficiente para que todos ellos estén justificados.
El espacio natural para buscar la solución del problema
Para obtener la formulación variacional de
Por tanto, para cada
Problema aproximado
Vamos a utilizar una aproximación mediante elementos finitos
con
cuya dimensión es igual al número de vértices de
Para cada
Resolución con FreeFEM
Tomaremos como
Consideramos una partición de intervalo
Construcción del mallado
Declaramos primero una variable tipo mesh y después construimos una triangulación del dominio usando square.
// Triangulacionint[int] La = [1,1,1,1];mesh Th = square(30, 30, flags = 3, label = La);plot(Th, wait = 1); 
Definición del espacio de elementos finitos
Definimos el espacio de elementos finitos que vamos a utilizar sobre
// Definicion del espacio de EFfespace Wh(Th, P1);Definición del problema variacional
Se recuerda que las condiciones de Dirichlet (en este caso
Dado uold.
// Declaracion de las variables del problema (elementos de Wh)Wh u, v, uold, u0 = sin(x), f = x*y;Obsérvese que en cada etapa de tiempo tenemos que resolver un problema variacional del mismo tipo. Para definir el problema usando problem , usaremos el parámetro opcional init que permite resolver varios problemas con la misma forma bilineal construyendo y factorizando la matriz del sistema una sola vez:
problem Calor(u, v, init = bool)
init = false(valor por defecto) la matriz se construye y se factoriza en cada problema,init = true, la matriz se construye y se factoriza solo en el primer problema; en los siguientes se utiliza la matriz ya factorizada.
// Definicion del problema aproximadoproblem Calor(u,v, init = 1) = int2d(Th)((dx(u)*dx(v)+dy(u)*dy(v))) + int2d(Th)(dt1*u*v) - int2d(Th)(dt1*uold*v) - int2d(Th)(f*v) + on(1, u = 0);Iteraciones en tiempo, resolución del problema y representación
Vamos a realizar un bucle en tiempo en el que, para cada
La estructura general del bucle indexado for es la siguiente:
for (inicializacion; condicion; incremento) { bloque de instucciones }donde
inicializaciones la inicialización del índice del bucle,condiciones una expresión con valor lógico: si toma valor verdadero (true), se repite el bloque de instrucciones, en caso contrario, no se repite,incrementoindica cómo cambia el índice del bucle de una iteración a otra,bloque de instuccioneses el conjunto de instrucciones a realizar.
Resolvemos el problema y representamos la solución en cada etapa de tiempo.
// Datosint M = 10;real T = 1., dt = T/M, dt1 = 1./dt;
// Iteraciones en tiempo u = u0;for (int n = 1; n <= M; ++n){ uold = u; Calor; plot(u, fill = true, dim = 3, wait = 1);} Obsérvese que el operador compuesto ++n incrementa en una unidad el valor de n . Además, puesto que los datos del problema no dependen de
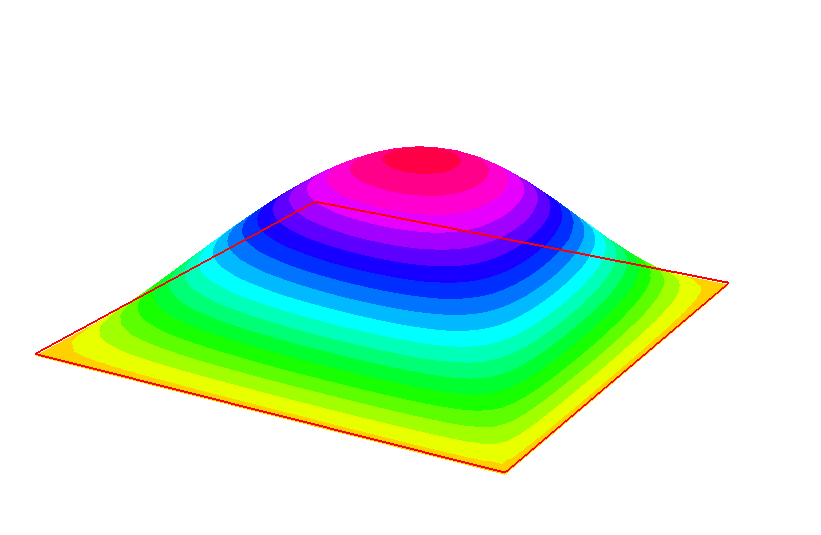
En la gráfica adjunta se puede observar la solución del problema en el tiempo final
Código completo del programa
// Datos real T = 1.;int M = 10; real dt = T/M, dt1 = 1./dt;
// Triangulacionint[int] La = [1,1,1,1];mesh Th = square(30, 30, flags = 3, label = La);plot(Th, wait = 1, ps = "MalladoCalor.eps");
// Espacio elementos finitosfespace Wh(Th, P1);Wh u, v, uold, u0 = sin(x), f = x*y;
// Definicion del problemaproblem Calor(u,v, init = 1) = int2d(Th)((dx(u)*dx(v)+dy(u)*dy(v))) + int2d(Th)(dt1*u*v) - int2d(Th)(dt1*uold*v) - int2d(Th)(f*v) + on(1, u = 0);
// Iteraciones en tiempou = u0;for (int n = 1; n <= M; ++n){ uold = u; Calor; plot(u, fill = true, dim = 3, wait = 1);} Ejercicios
- Resolver el problema
varf. - Sean
- Resolver el problema
varf. - Sean
donde
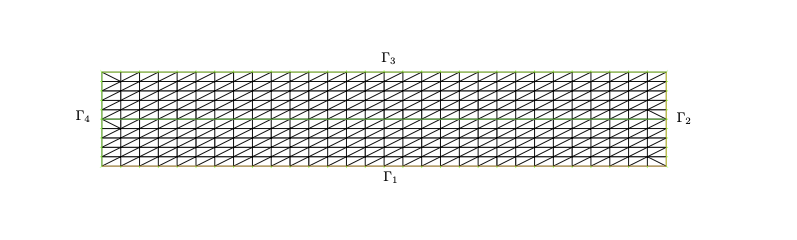
- Resolver el problema
- Resolver el problema
varf.
Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla