Lame2D.edp

Resumen: En este ejemplo se considera el problema estacionario de Lamé bidimensional.

Problema considerado

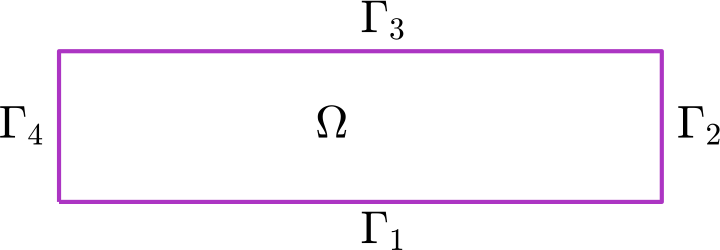
$\Omega \subset \mathbb{R}^2$ (que suponemos de frontera polígonal) un dominio ocupado por un medio elástico, isótropo y homogéneo que está sometido a una densidad de fuerzas externas, lo que produce una deformación del medio.

$\mathbf{u} = \mathbf{u}(x,y) = (u_1(x,y) ,u_2(x,y))$ $\mathbf{u}$ es solución del sistema

\begin{matrix} (1) & {\begin{cases} - \nabla \cdot σ (u) = f (x, y) & en Ω, \\ u = 0 & sobre Γ_{4}, \\ σ (u) \cdot n = g & sobre Γ_{1}, \\ σ (u) \cdot n = 0 & sobre Γ_{2} \cup Γ_{3}, \end{cases} \end{matrix}

donde

\begin{matrix} (2) & σ (u) = \frac{1}{2} μ (\nabla u + \nabla u^{t}) + λ (\nabla \cdot u) I d, \end{matrix}

$\lambda$ $\mu$ $E$ , denominado módulo de Youngmódulo de elasticidad longitudinal $\nu$ , denominado coeficiente o razón de Poisson:

\begin{matrix} (3) & μ = \frac{E}{2 (ν + 1)}, λ = \frac{E ν}{(ν + 1) (1 - 2 ν)} \end{matrix}

Formulación débil

$V = \{ \mathbf v\in H^1(\Omega)^2 \,\colon\, \mathbf v = 0 \quad\text{ sobre } \Gamma_4\}$ .

$\eqref{eq.Lame2D.1}$ $\mathbf v\in V$ $\Omega$ $\eqref{eq.Lame2D.1}$ :

\begin{matrix} (4) & {\begin{cases} Hallar u \in V tal que \\ \int_{Ω} (\frac{1}{4} μ (\nabla u + (\nabla u)^{t}) \cdot (\nabla v + (\nabla v)^{t}) + λ (\nabla \cdot u) (\nabla \cdot v)) d x d y \\ - \int_{Ω} f \cdot v d x d y - \int_{Γ_{1}} g \cdot v d σ = 0 \forall v \in V . \end{cases} \end{matrix}

$f(x,y) = \begin{pmatrix} 0 \\ -1 \end{pmatrix}$ $g(x,y)= \begin{pmatrix} 0 \\ x/10 \end{pmatrix}$ $E=21\times 10^5$ $\nu = 0.28$ .

Observamos que:

\begin{matrix} (5) & \begin{aligned} (\nabla u + (\nabla u)^{t}) & \cdot (\nabla v + (\nabla v)^{t}) \\ = (\begin{array}{c} 2 \partial_{x} u_{1} & \partial_{y} u_{1} + \partial_{x} u_{2} \\ \partial_{y} u_{1} + \partial_{x} u_{2} & 2 \partial_{y} u_{2} \end{array}) \cdot (\begin{array}{c} 2 \partial_{x} v_{1} & \partial_{y} v_{1} + \partial_{x} v_{2} \\ \partial_{y} v_{1} + \partial_{x} v_{2} & 2 \partial_{y} v_{2} \end{array}) \\ = 4 \partial_{x} u_{1} \partial_{x} v_{1} + 2 (\partial_{y} u_{1} + \partial_{x} u_{2}) (\partial_{y} v_{1} + \partial_{x} v_{2}) + 4 \partial_{y} u_{2} \partial_{y} v_{2} \\ = 4 (\partial_{x} u_{1}, \partial_{y} u_{2}, \frac{1}{\sqrt{2}} (\partial_{y} u_{1} + \partial_{x} u_{2})) (\begin{array}{c} \partial_{x} v_{1} \\ \partial_{y} v_{2} \\ \frac{1}{\sqrt{2}} (\partial_{y} v_{1} + \partial_{x} v_{2}) \end{array}) \end{aligned} \end{matrix}

Código


//  Stationary Lame system of elasticity 
//  |  Find u = (u_1, u_2)
//  |- \nabla\cdot\sigma(u) = f   in \Omega                (beam, viga)
//  |  \sigma\cdot n        = g   on \Gamma_1              (botom)
//  |  \sigma\cdot n        = 0   on \Gamma_2\cup\Gamma_3  (right side and top)
//  |   u                   = 0   sobre \Gamma_4           (left side)
//  where:
//    \sigma(u) = 0.5\mu (\nabla u + \nabla u^T) + \lambda (\nabla \cdot u) Id.
//  Weak formulation:
//    \int_\Omega ( 0.25\mu(\nabla u + \nabla u^T)\cdot(\nabla v + \nabla v^T) + 
//                  \lambda(\nabla \cdot u)(\nabla \cdot u) )
//   -\int_\Omega f\cdot v  -  \int_\gamma_1  g\cdot v = 0   \forall v
//

//
//  Data:
//
verbosity = 0;
real E  = 21.e5, nu = 0.28;                // Young modulus, Poisson ratio
real mu = E/(2*(1+nu));                    // Lame coefficient
real lambda = E*nu/((1+nu)*(1-2*nu));      // Lame coefficient

func f1 =  0.;                             // External force
func f2 = -1.;
func g1 =  0.;                             // Surface force
func g2 =  0.1*x;

//
//  Auxiliary variables:
//
real usqrt2 = 1./sqrt(2.);
real scale = 100.;

//
//  Mesh:
//
int  nx = 20, ny = 10;
mesh Th = square(nx, ny, [20.*x, 2.*y-1.]);   // Domain: (0, 20) X (-1, 1)
plot(Th, cmm = "Mesh of the domain (0, 20) X (-1, 1)", wait = true);

//
//  Finite element space
//  [u1, u2]  : unknown
//  [v1, v2]  : function test
//
fespace Vh(Th, P2);
Vh u1, u2, v1, v2;
Vh f1h=f1, f2h=f2, g1h=g1, g2h=g2;

//
//  Macro definitions:
//  Macros can have arguments (like those ones) and MUST finish by  //
macro epsilon(u1,u2) [dx(u1),dy(u2),usqrt2*(dy(u1)+dx(u2))] // EOM    
macro div(u1,u2) (dx(u1)+dy(u2)) // EOM

//
//  Problem:
//
problem Lame2D([u1, u2],[v1, v2]) = 
        int2d(Th)(lambda*div(u1,u2)*div(v1,v2) + mu*(epsilon(u1,u2)' * epsilon(v1,v2)))
      - int2d(Th)(f1h*v1+ f2h*v2) 
      - int1d(Th,1)(g1h*v1+g2h*v2)
      + on(4, u1 = 0., u2 = 0.);
//
//  Solution:
//
Lame2D;

//
//  Plots
//
plot([u1,u2], coef = scale, cmm = "Displacements", wait = true);
plot(u1, fill=true, value=1, cmm = "X-Displacement", wait = true);
plot(u2, fill=true, value=1, cmm = "Y-Displacement", wait = true);

mesh Thd = movemesh(Th, [x+scale*u1, y+scale*u2]);
int[int] re = [1,6,2,6,3,6,4,6,0,6], reg = [0,6];
//  Changing labels of original mesh for the plot
Th = change(Th, refe = re, region = reg);
plot(Th, Thd, cmm="Original and deformed mesh. Displacement multiplied by " + scale, wait=true);

Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla