Lame3D.edp

Resumen: En este ejemplo se considera el problema estacionario de Lamé 3D.

Problema

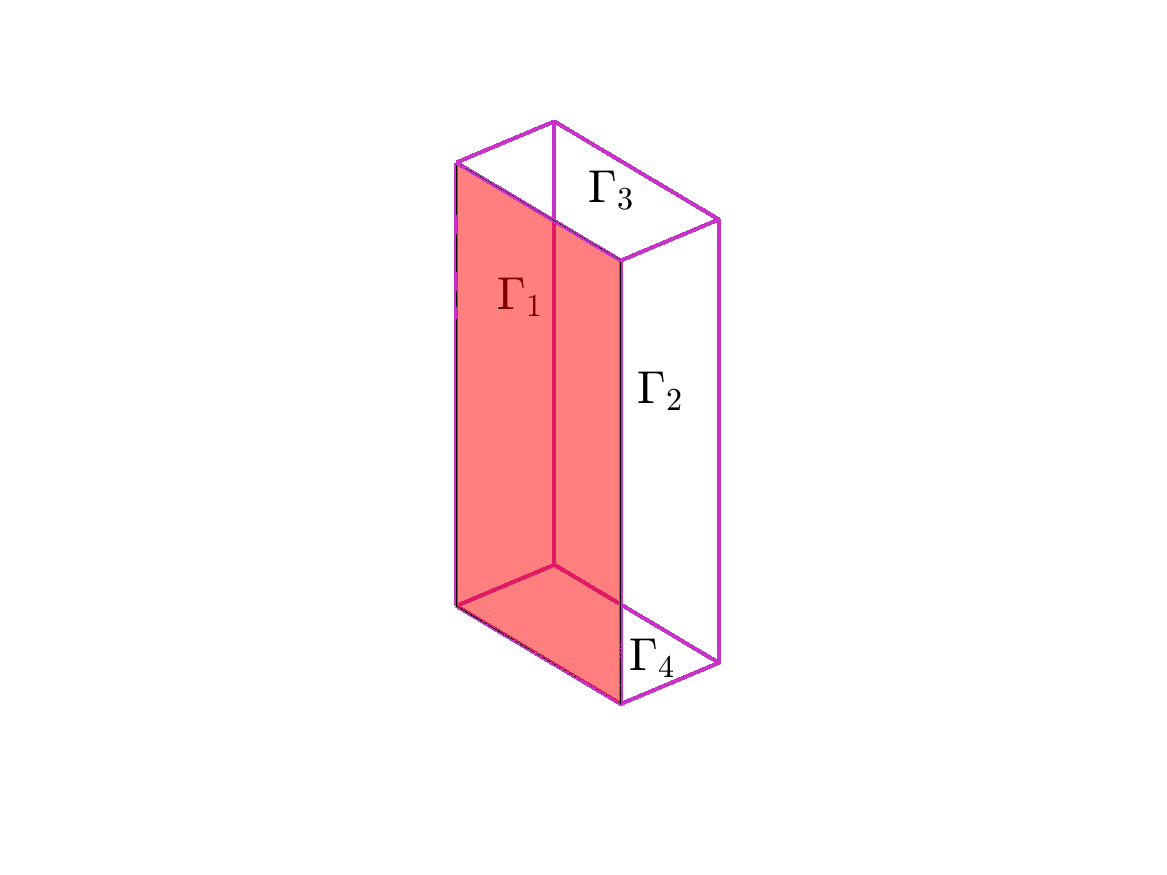
$\Omega \subset \mathbb{R}^3$ (que suponemos de frontera poliédrica) un dominio ocupado por un medio elástico, isótropo y homogéneo que está sometido a una densidad de fuerzas externas, lo que produce una deformación del medio.

$\mathbf{u} = \mathbf{u}(x,y,z) = (u_1(x,y,z) ,u_2(x,y,z))$ $\mathbf{u}$ es solución del sistema

\begin{matrix} (1) & {\begin{cases} - \nabla \cdot σ (u) = f (x, y, z) & en Ω, \\ u = 0 & sobre Γ_{4}, \\ σ (u) \cdot n = g & sobre Γ_{1}, \\ σ (u) \cdot n = 0 & sobre Γ_{2} \cup Γ_{3}, \end{cases} \end{matrix}

donde

\begin{matrix} (2) & σ (u) = \frac{1}{2} μ (\nabla u + \nabla u^{t}) + λ (\nabla \cdot u) I d, \end{matrix}

$\lambda$ $\mu$ $E$ , denominado módulo de Youngmódulo de elasticidad longitudinal $\nu$ , denominado coeficiente o razón de Poisson:

\begin{matrix} (3) & μ = \frac{E}{2 (ν + 1)}, λ = \frac{E ν}{(ν + 1) (1 - 2 ν)} \end{matrix}

Formulación débil

$V = \{ \mathbf v\in H^1(\Omega)^3 \,\colon\, \mathbf v = 0 \quad\text{ sobre } \Gamma_4\}$ .

$\eqref{eq.Lame2D.1}$ $\mathbf v\in V$ $\Omega$ $\eqref{eq.Lame2D.1}$ :

\begin{matrix} (4) & {\begin{cases} Hallar u \in V tal que \\ \int_{Ω} (\frac{1}{4} μ (\nabla u + (\nabla u)^{t}) \cdot (\nabla v + (\nabla v)^{t}) + λ (\nabla \cdot u) (\nabla \cdot v)) d x d y d z \\ - \int_{Ω} f \cdot v d x d y - \int_{Γ_{1}} g \cdot v d σ = 0 \forall v \in V . \end{cases} \end{matrix}

$f(x,y) = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$ $g(x,y)= \begin{pmatrix} -z \\0 \\ 0 \end{pmatrix}$ $E=21\times 10^5$ $\nu = 0.28$ .

Observamos que:

\begin{matrix} (5) & \begin{aligned} (\nabla u & + (\nabla u)^{t}) \cdot (\nabla v + (\nabla v)^{t}) \\ = (\begin{array}{c} 2 \partial_{x} u_{1} & \partial_{y} u_{1} + \partial_{x} u_{2} & \partial_{z} u_{1} + \partial_{x} u_{3} \\ \partial_{x} u_{2} + \partial_{y} u_{1} & 2 \partial_{y} u_{2} & \partial_{z} u_{2} + \partial_{y} u_{3} \\ \partial_{x} u_{3} + \partial_{z} u_{1} & \partial_{y} u_{3} + \partial_{z} u_{2} & 2 \partial_{z} u_{3} \end{array}) \cdot (\begin{array}{c} 2 \partial_{x} v_{1} & \partial_{y} v_{1} + \partial_{x} v_{2} & \partial_{z} v_{1} + \partial_{x} v_{3} \\ \partial_{x} v_{2} + \partial_{y} v_{1} & 2 \partial_{y} v_{2} & \partial_{z} v_{2} + \partial_{y} v_{3} \\ \partial_{x} v_{3} + \partial_{z} v_{1} & \partial_{y} v_{3} + \partial_{z} v_{2} & 2 \partial_{z} v_{3} \end{array}) \\ = 4 \partial_{x} u_{1} \partial_{x} v_{1} + 4 \partial_{y} u_{2} \partial_{y} v_{2} + 4 \partial_{z} u_{3} \partial_{z} v_{3} + \\ 2 (\partial_{y} u_{1} + \partial_{x} u_{2}) (\partial_{y} v_{1} + \partial_{x} v_{2}) + \\ 2 (\partial_{z} u_{1} + \partial_{x} u_{3}) (\partial_{z} v_{1} + \partial_{x} v_{3}) + \\ 2 (\partial_{z} u_{2} + \partial_{y} u_{3}) (\partial_{z} v_{2} + \partial_{y} v_{3}) \\ = 4 ε (u 1, u 2, u 3)^{t} \cdot ε (v 1, v 2, v 3) \end{aligned} \end{matrix}

con

\begin{matrix} (6) & \begin{matrix} ε (u 1, u 2, u 3) = (\begin{matrix} \partial_{x} u_{1} \\ \partial_{y} u_{2} \\ \partial_{y} u_{3} \\ \frac{1}{\sqrt{2}} (\partial_{y} u_{1} + \partial_{x} u_{2}) \\ \frac{1}{\sqrt{2}} (\partial_{z} u_{1} + \partial_{x} u_{3}) \\ \frac{1}{\sqrt{2}} (\partial_{z} u_{2} + \partial_{y} u_{3}) \end{matrix}) \end{matrix} \end{matrix}

Código


xxxxxxxxxx
//  Solution of stationary 3D Lame system of elasticity
//  | - \nabla \cdot \sigma(u) = f in \Omega = (0,1)x(0,2)x(0,4) 
//  |   \sigma(u) \cdot n = g      on \Gamma_1             (x=1 side)
//  |   \sigma(u) \cdot n = 0      on \Gamma_2\cup\Gamma_3 (other sides and top)
//  |   u = 0                      on \Gamma_4             (base)
//   \sigma(u) = 0.5\mu (\nabla u + \nabla u^T) + \lambda (\nabla \cdot u) Id.
//  Weak formulation
//    \int_\Omega ( 0.25\mu(\nabla u + \nabla u^T)\cdot(\nabla v + \nabla v^T) + 
//                  \lambda(\nabla \cdot u)(\nabla \cdot u) )
//   -\int_\Omega f\cdot v  -  \int_\gamma_1  g\cdot v = 0   \forall v

load "msh3" 
verbosity = 10;
    
//
//  Data
//
real E  = 21.e5;                            // Young modulus
real nu = 0.28;                             // Poisson ratio
real mu     = E/(2.*(1.+nu));               // Lame coefficients
real lambda = E*nu/((1.+nu)*(1.-2.*nu));    // Lame coefficients
real gamma1=mu, gamma2=mu+lambda;           // Other coefficients

func f1 = 0.;                               // External force
func f2 = 0.;                               // External force
func f3 = 0.;                               // External force
func g1 = -z;                               // Surface force
func g2 = 0.;                               // Surface force
func g3 = 0.;                               // Surface force

//
//  Auxiliary variables
//
real unsq2=1./sqrt(2.), coef=100.;

//
//  Macro definitions
//  macros MUST be ended by //
macro epsilon(u1, u2, u3) [dx(u1), dy(u2), dz(u3),
    unsq2*(dy(u1)+dx(u2)), unsq2*(dz(u1)+dx(u3)), unsq2*(dz(u2)+dy(u3))] // EOM
macro div(u1, u2, u3) (dx(u1) + dy(u2) + dz(u3)) // EOM

//
//  2D Mesh
//  Base domain : (0,1) x (0,2)
real x0 = 0., x1 = 1.;
real y0 = 0., y1 = 2.;
int nx = 5, ny = 10, nz = 20;           // steps in directions x, y, z
int L2 = 1, L0 = 9;                     // 2D labels: C2 --> L2, C1,C3,C4 --> L0

border C1(s = x0, x1){x = s;  y = y0;  label = L0;}
border C2(s = y0, y1){x = x1; y = s;   label = L2;}
border C3(s = x1, x0){x = s;  y = y1;  label = L0;}
border C4(s = y1, y0){x = x0; y = s;   label = L0;}
plot(C1(nx) + C2(ny) + C3(nx) + C4(ny), wait = true);

mesh Th2d = buildmesh(C1(nx) + C2(ny) + C3(nx) + C4(ny));
plot(Th2d, wait=true);

//
//  3D mesh
//  Domain:  (0,1) x (0,2) x (0,4)
real z0 = 0., z1 = 4.;
int Ltop = 13, Lbase = 15;    
int[int] rup   = [0, Ltop,L0, L0, L2, L2],  // upper face --> Ltop
     rdown = [0, Lbase, L0, L0, L2, L2],    // lower face --> Lbase
     rmid  = [L0, L0, L2, L2];              // lateral faces, L0 --> L0,  L2 --> L2
mesh3 Th3d = buildlayers(Th2d, nz, zbound = [z0,z1],
                     labelmid  = rmid, 
                     labelup   = rup, 
                     labeldown = rdown);
plot(Th3d, wait = true);

//
//  Finite element space
//
fespace Vh(Th3d,P2);
Vh u1, u2, u3;
Vh v1, v2, v3;
Vh f1h = f1, f2h = f2, f3h = f3;
Vh g1h = g1, g2h = g2, g3h = g3;

//
//  Problem
//
problem Lame3D([u1, u2, u3],[v1, v2, v3]) = 
          int3d(Th3d)( lambda*(div(u1, u2, u3)*div(v1, v2, v3))
        + mu*(epsilon(u1, u2, u3)'*epsilon(v1, v2, v3)) )
        - int3d(Th3d)(f1h*v1 + f2h*v2 + f3h*v3) 
        - int2d(Th3d,L2)(g1h*v1 + g2h*v2 + g3h*v3)
        + on(Lbase, u1 = 0., u2 = 0., u3 = 0.);
Lame3D;

//
//  Plots
//
mesh3 Th3dd = movemesh3(Th3d, transfo = [x+coef*u1, y+coef*u2, z+coef*u3]);

int[int] re = [L0,0, L2,0, Ltop,0, Lbase,0], reg = [0,6];
//  Changing labels of original mesh for the plot
Th3d = change(Th3d, refface = re);
plot(Th3d, Th3dd, cmm = "Original and deformed mesh. Displacement multiplied by "+coef, wait = true);

Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla