Construcción de mallados

Resumen: Se presentan algunos ejemplos de definición dominios y la construcción de sus mallados.

Mallados 2D

Círculo

Tomaremos como dominio Ω$\Omega$​​ el interior de un círculo de centro el origen y radio 2, siendo su frontera ∂Ω$\partial\Omega$ definida por la curva

Las siguientes instrucciones definen la frontera del dominio, utilizando ecuaciones paramétricas. Obsérvese que hemos asignado la etiqueta 14 a dicha curva con la instrucción label = 14. Se recomienda siempre la asignación de etiquetas a las fronteras (más adelante se verá su uso).

// Definicion de la frontera del dominio
border C(t = 0, 2*pi){x = 2*cos(t); y = 2*sin(t); label = 14;};

Obsérvese que, para dibujar la curva C$C$ se han usado las variables reservadas x e y que representan, en FreeFEM, las dos coordenadas espaciales.

Para dibujar dicha curva usamos el comando plot ver aquí las explicaciones de su uso. Escribiendo C(30) indicamos que la curva C$C$ se aproxima mediante una poligonal formada por 30 segmentos de igual longitud.

// Representacion de la frontera del dominio
plot(C(30), wait = 1);  

Se observa que, según la parametrización que se ha hecho, la frontera se recorre en el sentido directo (contrario a las agujas del reloj). Obsérvese la diferencia si se define el borde haciendo variar t desde 2*pi hasta 0 .

// Definicion de la frontera del dominio
border C1(t = 2*pi, 0){x = 2*cos(t); y = 2*sin(t); label = 15;};
plot(C1(30), wait = 1);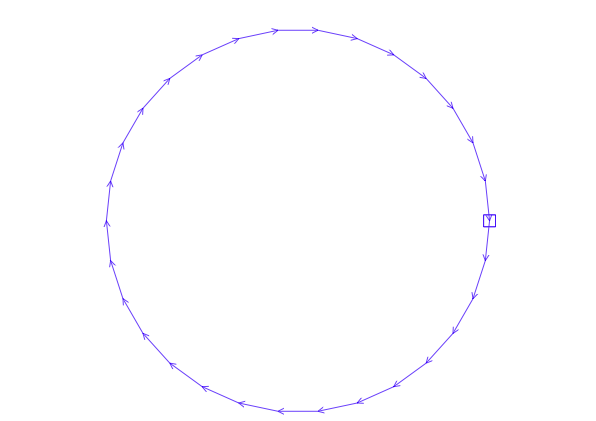

Para construir el mallado, declaramos primero una variable de tipo mesh , y después construimos una triangulación del dominio encerrado por la curva C$C$ discretizada con 30 segmentos. Para que FreeFEM entienda bien el papel de la frontera, debemos respetar una regla: el dominio debe quedar siempre a la izquierda cuando se recorre la frontera.

// Construccion de la triangulacion
mesh Th;
Th = buildmesh(C(30));
plot(Th, wait = 1);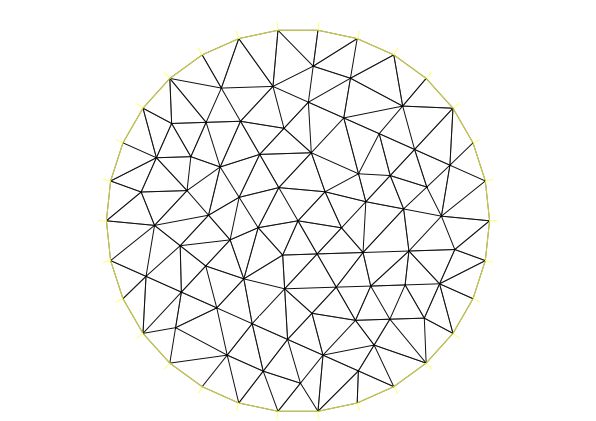

Se observa que no es posible construir una triangulación del dominio definido por el borde C1 que aparece más arriba, puesto que el dominio que queda a la izquierda cuando se recorre la frontera C1 es el exterior del círculo y no está acotado. En una situación como esta, para arreglar el problema, basta indicar un número negativo de segmentos sobre la frontera para construir el mallado:

// Construccion de la triangulacion usando el borde C1
mesh T1h; 
T1h = buildmesh(C1(-30));
plot(T1h, wait = 1);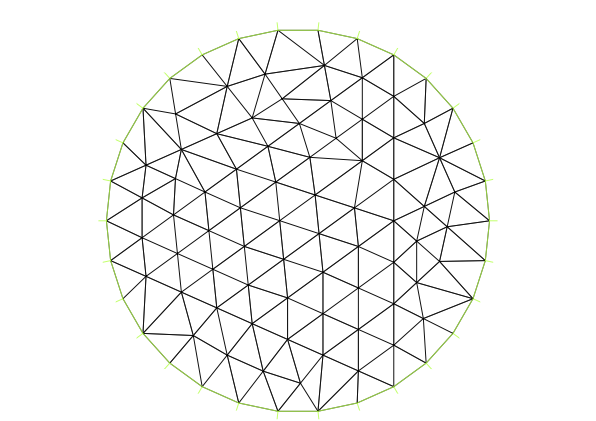

Círculo con frontera compuesta de dos partes

Tomaremos como dominio Ω$\Omega$​​ el interior de un círculo de centro (1,0)$(1,0)$ y radio 1, siendo su frontera ∂Ω=Γ1∪Γ2$\partial\Omega=\Gamma_1\cup\Gamma_2$, definida por las curvas

Las siguientes instrucciones definen las dos partes de la frontera del dominio, utilizando de nuevo ecuaciones paramétricas. Obsérvese que hemos asignado las etiquetas label = 1 y label = 10 a dichas curvas:

// Definicion de la frontera del dominio
real pi2 = pi/2;
border Gamma1(t = 0, pi2){x = 1+ cos(t); y = sin(t); label = 1;};
border Gamma2(t = pi2, 2*pi){x = 1 + cos(t); y = sin(t); label = 10;};
plot(Gamma1(10) + Gamma2(30), wait = 1, ps = "Circulo2.eps");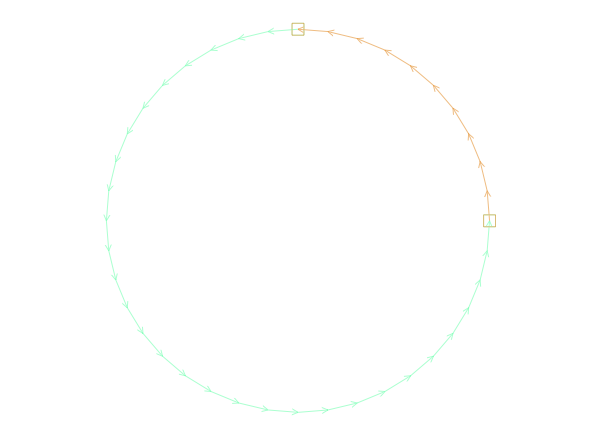

Para construir el mallado, se procede como en el ejemplo anterior, teniendo en cuenta ahora que la frontera es compuesta. Por ejemplo, elegiremos para Γ1$\Gamma_1$ una distretización con 10 segmentos y para Γ2$\Gamma_2$ una con 30 segmentos. Podemos declarar y definir el mallado en la misma instrucción:

// Construccion de la triangulacion
mesh Ch = buildmesh(Gamma1(10) + Gamma2(30));
plot(Ch, wait = 1, ps = "MalladoCirculo2.eps");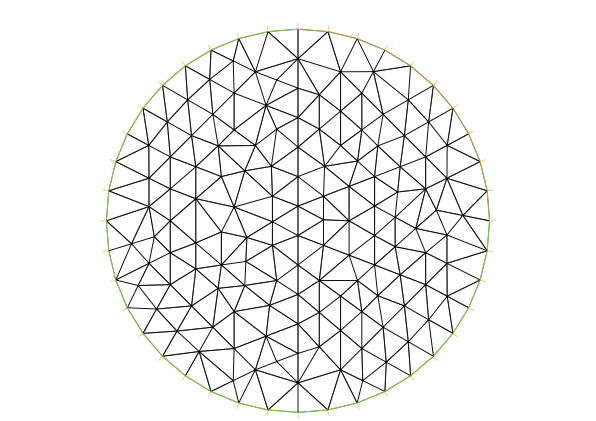

Cuadrado

El comando square permite construir un mallado de un dominio rectangular. En su uso más básico, permite generar un mallado del cuadrado [0,1]×[0,1]$[0,1]\times [0,1]$ :

mesh Qh = square(n, m);

donde el significado de los parámetros obligatorios n y m es el siguiente:

• n es el número de segmentos en [0,1]$[0,1]$ a lo largo del eje OX,
• m es el número de segmentos en [0,1]$[0,1]$ a lo largo del eje OY.

Por ejemplo, un mallado 4×5$4\times 5$ del cuadrado [0,1]×[0,1]$[0,1]\times[0,1]$ se crea con los comandos que siguen:

xxxxxxxxxx
// Mallado del cuadrado [0,1]x[0,1]
mesh Sh = square(4,5);
plot(Sh, wait = 1);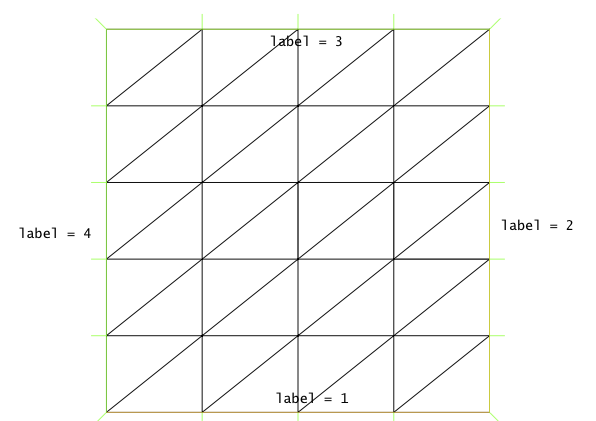

Se observa que, por defecto, se asignan las etiquetas 1, 2, 3 y 4 a los 4 lados del cuadrado, en el orden que se indica en la figura.

Rectángulo

Para construir un mallado n×m$n \times m$ del rectángulo [x0,x1]×[y0,y1]$[x_0,x_1]\times [y_0,y_1]$, se utiliza el comando square en su forma más general:

xxxxxxxxxx
mesh Rh = square(n, m, [x0+(x1-x0)*x, y0+(y1-y0)*y]);

Por ejemplo, un mallado 5×20$5\times 20$ del rectángulo [1.2,2]×[0.5,1.5]$[1.2, 2]\times [0.5, 1.5]$ se define como sigue:

xxxxxxxxxx
// Mallado de rectangulo [x0,x1]x[y0,y1]
real x0 = 1.2, x1 = 2.;
real y0 = 0.5, y1 = 1.5;
int n = 5, m = 20;
mesh Rh = square(n, m, [x0+(x1-x0)*x, y0+(y1-y0)*y]);
plot(Rh, wait = 1);

La forma mas completa del comando square es:

xxxxxxxxxx
mesh Th = square(n, m, [x0+(x1-x0)*x,y0+(y1-y0)*y], flags = iC, label = La, region = id);

Donde los parámetros (opcionales) son :

• flags= iC indica el tipo de mallado que se va a realizar, siendo flags = 0 la opción por defecto. Los otros cuatro posibles valores de flags son 1, 2, 3, 4 , cuyo resultado se puede observar en las figuras siguientes

  flags = 0
  flags = 1
  flags = 2
  flags = 3
  flags = 4

• label = La , donde La es un vector fila de cuatro elementos que define las etiquetas para las 4 fronteras.

• region = id , permite asignar un número de identificación a la región interior al cuadrado.

Ejercicios

Ejercicio 1

Sea Ω$\Omega$ el interior del anillo formado por un círculo de centro el origen y radio 2 y el círculo de centro el origen y radio 1. Tenemos ∂Ω=Γ1∪Γ2$\partial\Omega = \Gamma_1\cup \Gamma_2$​​ con

Construir un mallado de Ω$\Omega$, tomando una partición de Γ1$\Gamma_1$ de 50 segmentos y 20 sobre Γ2$\Gamma_2$.

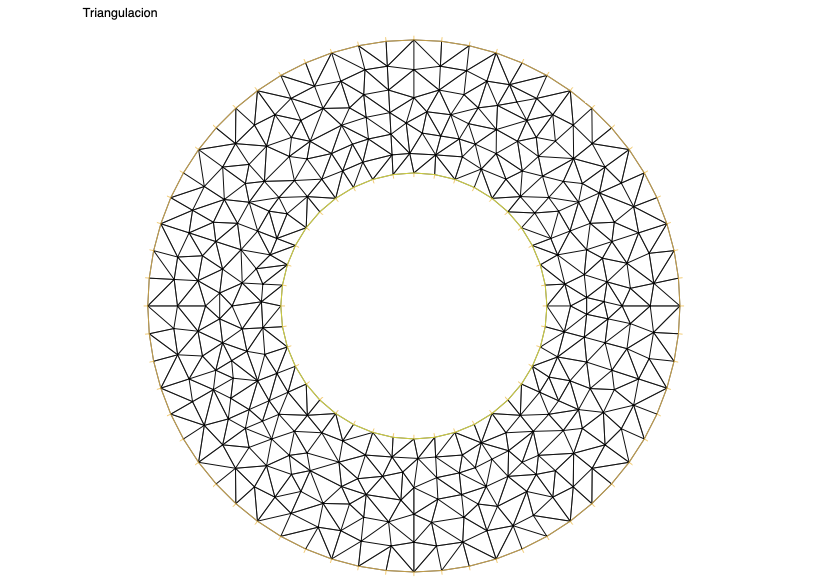
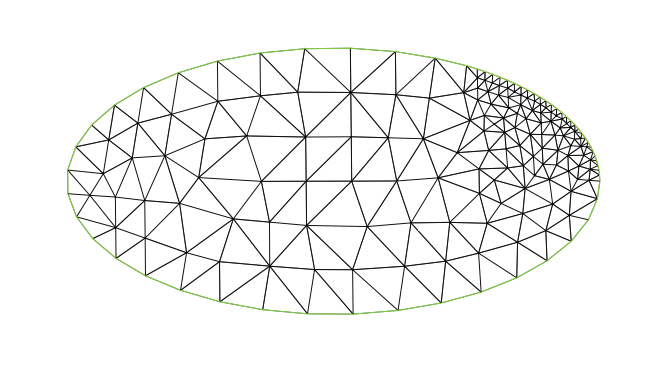
Ejercicio 2

Construir un mallado del dominio Ω$\Omega$​ siendo Ω$\Omega$ el interior de una elipse cuya frontera ∂Ω=Γ1∪Γ2$\partial\Omega = \Gamma_1\cup \Gamma_2$​​​ viene definida por las curvas

Utilizar distinto número de segmentos para discretizar Γ1$\Gamma_1$ y Γ2$\Gamma_2$.

Adaptación del mallado

La adaptación del mallado es una herramienta muy útil cuando la solución de un problema tiene importantes variaciones en una zona determinada del dominio. El comando adaptmesh permite adaptar el mallado a esta circunstancia, de modo que el mallado inicial se hace "más fino" en la parte en la que se producen grandes variaciones de la función.

El uso básico del comando adaptmesh es

mesh ThNew = adaptmesh(Th, f);

donde el significado de los argumentos es el que sigue:

• Th es el mallado inicial a adaptar,
• f es una función de tipo func o una función de tipo fespace del espacio de elementos finitos.
• ThNew es el nuevo mallado adaptado.

El papel desempeñado por f es el de fijar una "métrica" en base a la cual:

(a) en la zona donde f experimenta grandes variaciones (es decir, su gradiente es "grande") se refina el mallado, y

(b) por el contrario, allá donde f es aproximadamente constante, se usan triángulos de gran tamaño (si es necesario, incluso se suprimen triángulos anteriormente construidos).

Ejemplo 1: Consideramos la siguiente función en un mallado 5×5$5\times 5$ del cuadrado [0,1]2$[0,1]^2$:

En el código que sigue se realiza la adaptación del mallado dos veces:

​x
// Ejemplo 1 (adaptacion del mallado)
mesh Th = square(5,5);
plot(Th, wait = true, cmm = "Ejemplo 1: Mallado original");

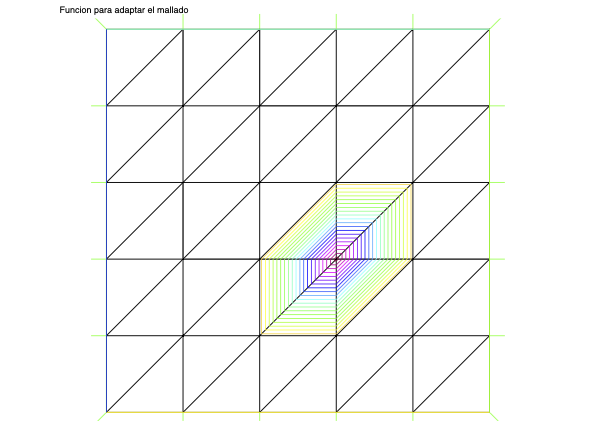
// Funcion para adaptar
real sigma  = 0.001, qx = 0.65, qy = 0.35, sigma2 = - 0.5 / sigma;
func fg = 3 * exp(sigma2*((x-qx)^2+(y-qy)^2));
fespace Vh(Th, P1);
Vh g = fg;
plot(Th, g, wait = true, cmm = "Funcion para adaptar el mallado");

// Adaptacion del mallado 1
Th = adaptmesh(Th, fg);
g = fg;
plot(Th, g, wait = true, cmm = "adaptmesh: 1 iteracion");

// Adaptacion del mallado 2
Th = adaptmesh(Th, fg);
g = fg;
plot(Th, g, wait = true, cmm = "adaptmesh: 2 iteraciones");

El uso algo más completo del comando adaptmesh es el que sigue

mesh ThNew = adaptmesh(Th, f, err = Error );

donde el parámetro err toma un valor real Error que indica el nivel del error de interpolación P1$P_1$ (el valor por defecto es 0.01).

Ejemplo 2: Consideramos la siguiente función en un mallado 5×5$5\times 5$ del cuadrado [−1,1]2$[-1,1]^2$:

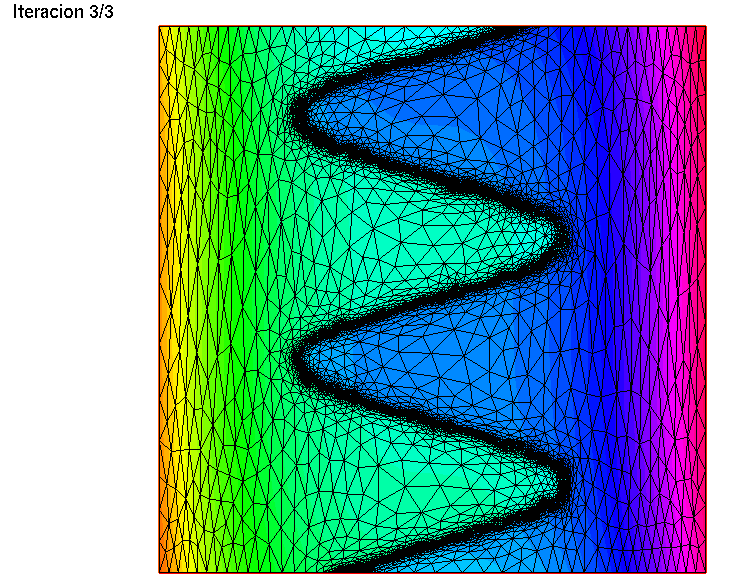
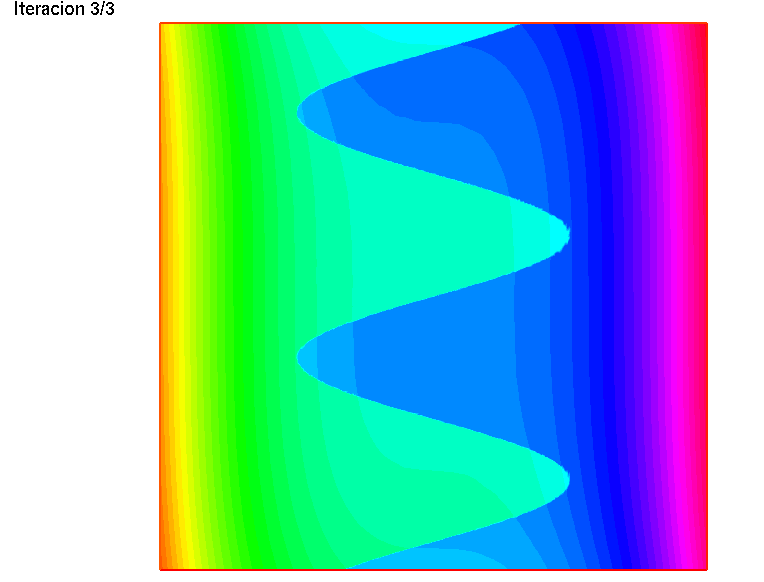
En el código que sigue se realiza la adaptación del mallado tres veces, haciendo disminuir el parámetro del error en cada iteración de la adaptación.

xxxxxxxxxx
// Ejemplo 2 (adaptacion del mallado)
real eps   = 0.0001;
real Error = 0.01;  
//  atan2(y, x) = arctag(y/x)
func f = 10.*x^3 + y^3 + atan2(eps, sin(7.0*y)-2.0*x);

// Mallado
mesh Th = square(5, 5, [-1+2*x, -1+2*y]);

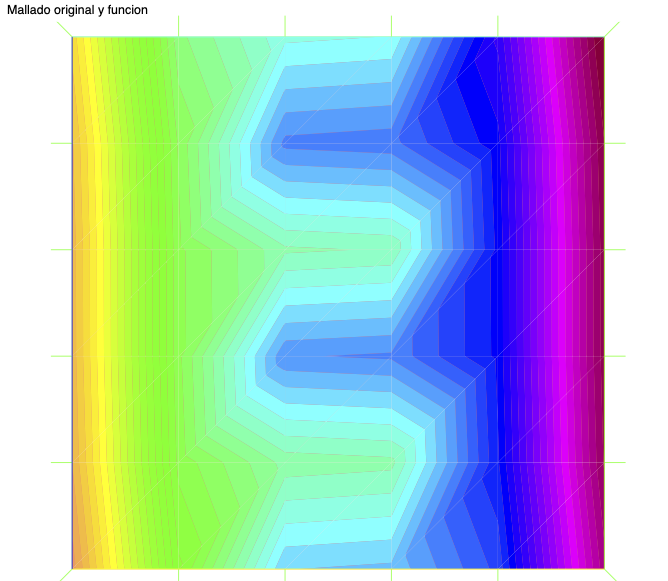
// Espacio de elementos finitos
fespace Vh(Th,P1);
Vh fh = f;
plot(Th, fh, nbiso=50, cmm = "Mallado original y funcion",  fill = true, wait = true);

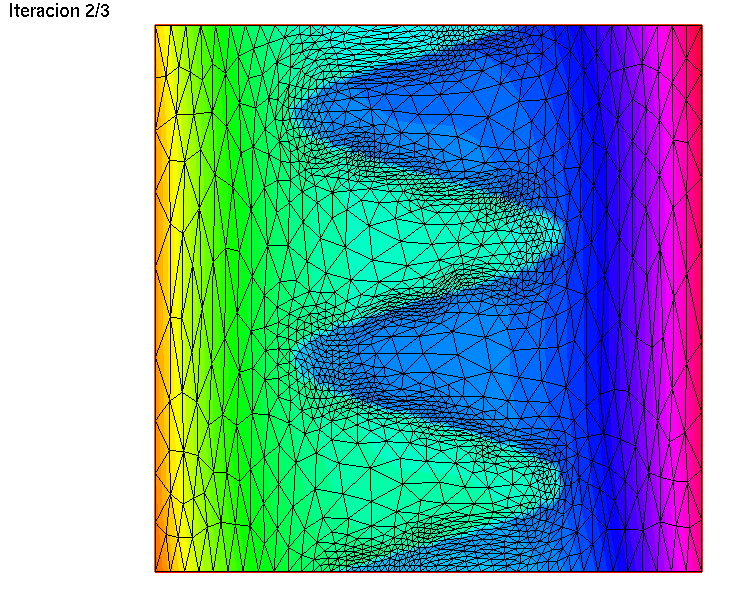
// Adaptacion del mallado
int niter = 3;
for (int i = 0; i < niter; i++){
    Th = adaptmesh(Th, fh, err= Error);
    Error /= 2;
    fh = f;
    plot(Th, fh, nbiso=50, fill = true, cmm = "Iteracion "+ (i+1)+"/"+niter, wait=true);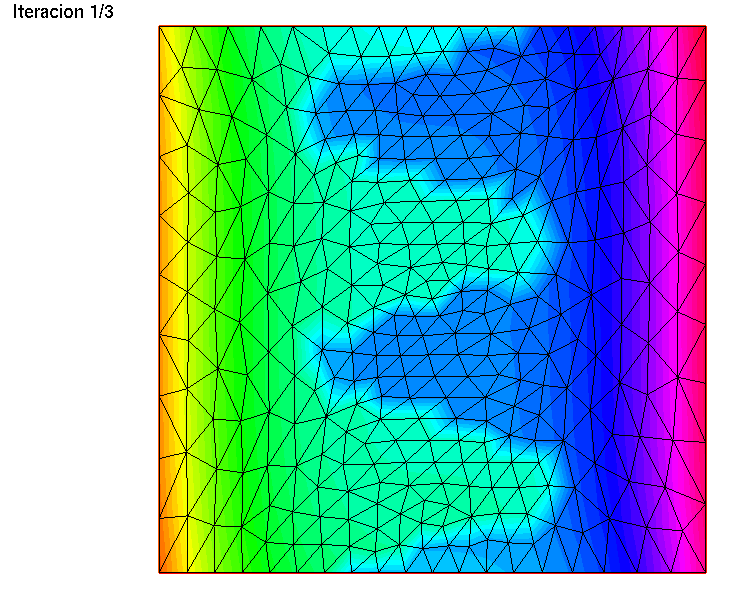
}

Mallados 3D

Cubo

Para construir mallados en tres dimensiones hay que escribir al comienzo del programa la orden

load "msh3"

El comando cube permite construir un mallado de un cubo. Su uso más básico permite generar un mallado del cubo [0,1]×[0,1]×[0,1]$[0,1]\times [0,1]\times [0,1]$ :

xxxxxxxxxx
mesh3 Th1 = cube(n, m, k);

donde el significado de los parámetros obligatorios n , m y k es

• n es el número de segmentos en [0,1]$[0,1]$ a lo largo del eje OX,
• m es el número de segmentos en [0,1]$[0,1]$ a lo largo del eje OY,
• k es el número de segmentos en [0,1]$[0,1]$ a lo largo del eje OZ,

Por ejemplo, un mallado 3×4×5$3\times 4\times 5$ del cubo [0,1]3$[0,1]^3$ se crea con los comandos que siguen.

xxxxxxxxxx
// Mallado del cubo [0,1]x[0,1]x[0,1]
load "msh3"
mesh3 Th1 = cube(3, 4, 5);
plot(Th1, wait = true);

Por defecto las etiquetas asignadas son:

• Cara y = 0 →$\rightarrow$ label = 1,
• Cara x = 1 →$\rightarrow$ label = 2,
• Cara y = 1 →$\rightarrow$ label = 3,
• Cara x = 0 →$\rightarrow$ label = 4,
• Cara z = 0 →$\rightarrow$ label = 5,
• Cara z = 1 →$\rightarrow$ label = 6,
• Región interior →$\rightarrow$ label = 0.

Paralelepípedo rectangular

Para construir un mallado n×m×k$n \times m\times k$ de un paralelepípedo rectangular [x0,x1]×[y0,y1]×[z0,z1]$[x_0,x_1]\times [y_0,y_1]\times [z_0,z_1]$, se utiliza el comando cube en su forma más general.

xxxxxxxxxx
mesh3 Th2 = cube(n, m, k, [x0+(x1-x0)*x, y0+(y1-y0)*y, z0+(z1-z0)*z]);

Por ejemplo, un mallado 5×4×6$5\times 4\times 6$ del dominio [−1,1]×[1,2]×[2,3]$[-1, 1]\times [1,2]\times[2,3]$ se define como sigue

xxxxxxxxxx
// Mallado de [x0,x1]x[y0,y1]x[z0,z1]
load "msh3"
real x0 = -1., x1 = 1.;
real y0 = 1., y1 = 2.;
real z0 = 2., z1 = 3.;
mesh3 Th2 = cube(5,4,6, [x0+(x1-x0)*x, y0+(y1-y0)*y, z0+(z1-z0)*z]);
plot(Th2, wait = true);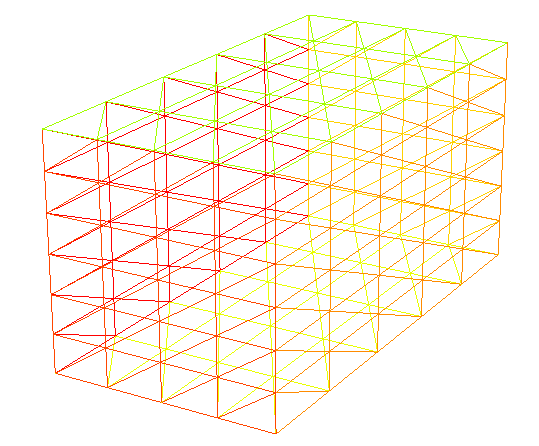

Una forma mas completa del comando cube es:

xxxxxxxxxx
mesh3 Th3 = cube(n, m, k, [x0+(x1-x0)*x, y0+(y1-y0)*y, z0+(z1-z0)*z], flags = iC, label = La, region = id);

donde el significado de los parámetros (opcionales) es similar al que se describe en el comando square. Por ejemplo, un mallado del cubo [0,1]3$[0,1]^3$ con las etiquetas de las caras personalizadas, puede observase en

xxxxxxxxxx
// Mallado del cubo [0,1]^3 
load "msh3"
int[int] L6 = [14, 1, 5, 20, 9, 0];
mesh3 Th3 = cube(3, 4, 5, label = L6, flags = 3);
plot(Th3, wait = true);

Cilindros

El comando buildlayer permite construir un mallado 3D extendiendo por capas un mallado bidimensional en la dirección del eje OZ. Por ejemplo, un mallado de un cilindro con base elíptica se consigue con los comandos

x
load "msh3"
  
// Mallado 2D (elipse)
int L1 = 14;
border elipse(t=0, 2*pi){x = cos(t); y = 2*sin(t); label = L1;};
mesh Thelipse = buildmesh(elipse(60));
plot(Thelipse, wait = true);

// Mallado 3D (cilindro)
int nz = 4;
real zmin = 0., zmax = 1.;
int[int] rup = [0, 9], rdown = [0, 20];
mesh3 Thcylinder = buildlayers(Thelipse, nz, zbound = [zmin, zmax],
                   labelup = rup, labeldown = rdown);
plot(Thcylinder, wait = true);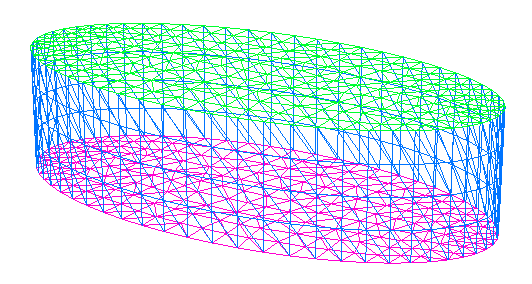       

Los parámetros que se han usado en buildlayers son:

• Thelipse indica nombre del mallado bidimensional que se va a extender por capas.
• nz es un entero que indica el número de capas, en este caso, igual a 4.
• zbound = [zmin, zmax] , siendo zmin(x,y) y zmax(x,y) dos funciones que definen, respectivamente, la superficie inferior (sobre la que reposa la cara inferior del dominio resultante) y la superficie superior (resp. la cara superior). En este caso, las funciones son constantes, iguales a 0 y 1, lo cual corresponde a superficies planas paralelas al plano XY$XY$.
• labeldown, labelmid, labelup son vectores formados por pares de números enteros: [NumOld, NumNew], donde NumOld hace referencia a la etiqueta del mallado 2D que se quiere cambiar por NumNew en el mallado 3D. Por defecto, los elementos de la cara inferior y superior del mallado 3D heredan la referencia de la región del mallado 2D, mientras que los elementos de la superficie lateral del cilindro heredan la referencia del borde del mallado 2D del que proceden. En estas asignaciones, los números de las etiquetas no se pueden proporcionar directamente a partir de constantes, sino que deben ser previamente asignados a variables adecuadas. En el caso del ejemplo, rup y rdown .

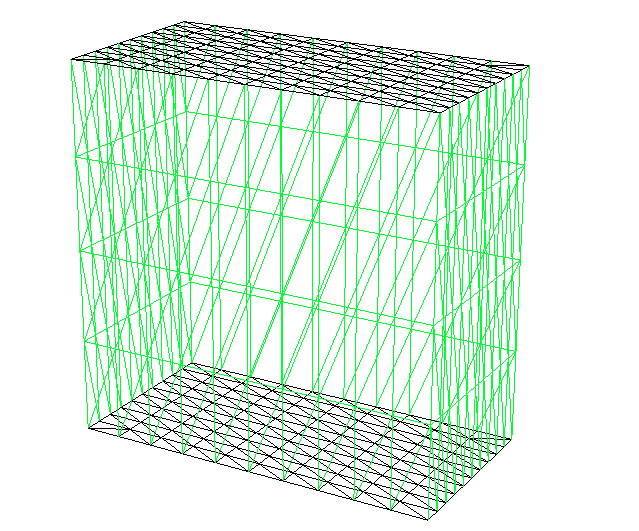
Ejercicio

Construir usando buildlayers , un mallado del dominio [0,1]×[0,2]×[−1,1]$[0, 1]\times[0,2]\times[-1,1]$ con 4 capas, poniendo la etiqueta 90 a la superficie de arriba y abajo y la etiqueta 9 a las superficies laterales (usando el parámetro labelmid).

Visualización

Resumen: Se presentan algunos métodos de visualización de los resultados obtenidos con FreeFEM.

Función plot

Esta función permite representar mallados y resultados obtenidos con FreeFEM. Su uso general es

xxxxxxxxxx

plot(Parametros obligatorios, parametros opcionales)
 

Algunos ejemplos de parámetros obligatorios son:

• Triangulacion (un objeto de tipo mesh o mesh3): el mallado a representar
• funcion (una función de un espacio de elementos finitos): la función a representar. Puede ser escalar o vectorial. Por ejemplo, la solución de un problema variacional.
• frontera : una discretización de un contorno construido con border.
• poligonal : un par de vectores reales [xu, yu] conteniendo respectivamente las abscisas y las ordenadas de los vértices de la poligonal (por ejemplo, para dibujar una curva).

Es posible incluir más de uno de los parámetros obligatorios, por ejemplo, un mallado junto con la solución de un problema.

Algunos de los parámetros opcionales son:

• wait = true / false wait = 1 / 0 Si es true o 1, se espera antes de continuar, hasta que se pulse return.
• ps = "fichero.ps" / "fichero.eps" Nombre del fichero para salvar la figura representada con plot (formato Postscript).
• fill = true / false Si es true, se rellenan con colores los espacios entre las líneas de nivel (solo para funciones fespace escalares).
• cmm = "comentario" Texto a incluir en la gráfica.
• value = true / false Si es true, se muestra la barra de colores (asociación color : valor).
• nbiso = numero Número de líneas de nivel a representar en la escala.
• boundary = true/false) Se es true, se dibuja la frontera del dominio (valor por defecto).
• dim = 2/3 Establece la dimensión de la gráfica 2 o 3.
• WindowIndex = numero Especifica el número de ventana para cuando hay varias ventanas gráficas.

Algunos atajos del teclado en la representación con plot son:

• enter para visualizar el siguiente gráfico cuando wait = true.
• p para mostrar el gráfico previo (hasta 10 gráficos anteriores).
• ? muestra la lista con todos los atajos del teclado.
• + , - acerca/aleja alrededor del cursor.
• = restablece la vista del gráfico inicial.
• up, down, left, right traslada el gráfico arriba, abajo, izquierda, derecha.
• 3 alterna entre vista 3d y 2d.
• z, Z en la representación 3d, aleja / acerca el gráfico.
• h, H en la representación 3d disminuye / aumenta la escala Z del gráfico.
• botón izquierdo del ratón permite rotar el gráfico.
• a, A disminuye / aumenta el tamaño de las flechas.
• B alterna entre mostrar el borde o no.
• n, N disminuye / aumenta el número de líneas de nivel.
• f alterna entre llenar con color o no el espacio entre líneas de nivel.
• l alterna entre iluminación o no.
• v alterna entre mostrar o no barra de colores (asociación color : valor).
• m alterna entre mostrar o no el mallado.
• esc cierra las ventana gráficas.

Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla