Ecuación de Poisson con condiciones mixtas Dirichlet-Neumann

Resumen: Se resuelve la ecuación de Poisson con condiciones de contorno mixtas Dirichlet-Neumann. Además, veremos dos formas diferentes de definir el problema variacional. Por un lado, usando el tipo solve que define el problema variacional y lo resuelve automáticamente. Por otro, usaremos el tipo varf , que define el problema variacional a través de la forma bilineal y la forma lineal. El problema considerado aparece, por ejemplo, para describir el desplazamiento vertical de una membrana que ocupa un dominio bajo una fuerza que actúa sobre ella.

Problema considerado

$\Omega\subset \mathbb{R}^2$ $\partial \Omega = \Gamma_1\cup \Gamma_2$ $f\in L^2(\Omega)$ $u_0\in L^2(\Gamma_1)$ $g\in L^2(\Gamma_2)$ $u:\Omega \to \mathbb{R}$ tal que

\begin{matrix} (P) & {\begin{cases} - Δ u = f & en Ω, \\ u = u_{0} & sobre Γ_{1}, \\ \frac{\partial u}{\partial n} = g & sobre Γ_{2} . \end{cases} \end{matrix}

Formulación variacional

Observación: todos los cálculos que se hacen en esta sección son puramente formales, es decir, se supone siempre la regularidad suficiente para que todos ellos estén justificados.

Introducimos el siguiente espacio de Hilbert

\begin{matrix} V = {v \in H^{1} (Ω) / v = 0 sobre Γ_{1}} . \end{matrix}

$\eqref{eq.membrana1}$ $\widetilde{u}_0+V$ $\widetilde{u}_0\in H^1(\Omega)$ $\widetilde{u}_0|_{\Gamma_1} = u_0$ .

$\eqref{eq.membrana1}$ $v\in V$ $\Omega$ , obteniendo

\begin{matrix} \int_{Ω} \nabla u \cdot \nabla v d x d y - \int_{\partial Ω} \frac{\partial u}{\partial n} v d σ = \int_{Ω} f v d x d y \forall v \in V . \end{matrix}

$\partial\Omega = \Gamma_1\cup \Gamma_2$ $v$ ${\Gamma_1}$ $\dfrac{\partial u}{\partial n} \bigg|_{\Gamma_2}=g$ , se obtiene:

\begin{matrix} \int_{Ω} \nabla u \cdot \nabla v d x d y - \int_{Γ_{2}} g v d σ = \int_{Ω} f v d x d y \forall v \in V . \end{matrix}

$\eqref{eq.membrana1}$ es, por tanto

\begin{matrix} (PV) & {\begin{cases} Hallar u \in {\tilde{u}}_{0} + V tal que \\ \int_{Ω} (\partial_{x} u \partial_{x} v + \partial_{y} u \partial_{y} v) d x d y = \int_{Ω} f v d x d y + \int_{Γ_{2}} g v d σ \forall v \in V . \end{cases} \end{matrix}

Problema aproximado

$P_1$ $\Omega$ $\mathcal{T}_h$ $\overline\Omega$ . Consideramos

\begin{matrix} W_{h} = {v_{h} | v_{h} \in C^{0} (\overset{―}{Ω}), v_{h} |_{T} \in P_{1} (T) \forall T \in T_{h}} \subset H^{1} (Ω) \end{matrix}

$\text{dim}\, W_h = M$ $M$ $\mathcal{T}_h$ . Consideramos también

\begin{matrix} V_{h} = {v_{h} | v_{h} \in W_{h}, v_{h} |_{Γ_{1}} = 0} \subset H_{1} (Ω), \end{matrix}

$\mathcal{T}_h$ no $\Gamma_1$ $\eqref{eq.membrana1.PV}$ es

\begin{matrix} (PV_{h}) & {\begin{cases} Hallar u_{h} \in {\tilde{u}}_{0 h} + V_{h} tal que \\ \int_{Ω} (\partial_{x} u_{h} \partial_{x} v_{h} + \partial_{y} u_{h} \partial_{y} v_{h}) d x d y = \int_{Ω} f v_{h} d x d y + \int_{Γ_{2}} g v_{h} d σ \forall v_{h} \in V_{h}, \end{cases} \end{matrix}

$\widetilde{u}_{0h}\in W_h$ $\widetilde{u}_{0h}(a_i)= \widetilde{u}_0(a_i)$ $a_i\in \Gamma_1$ .

Resolución con FreeFEM

$\Omega$ $\partial\Omega = \Gamma_1\cup \Gamma_2$ viene definida por las curvas

\begin{matrix} \begin{array}{l} Γ_{1} = {(x, y) : x = \cos (t), y = 2 \sin (t), 0 \leq t \leq π}, \\ Γ_{2} = {(x, y) : x = \cos (t), y = \sin (t), π \leq t \leq 2 π} . \end{array} \end{matrix}

$f(x,y) \equiv 1$ .

Definición de la frontera del dominio

Las siguientes instrucciones definen la frontera del dominio, utilizando sus ecuaciones paramétricas y la dibujan. Obsérvese que hemos asignado las etiquetas label = C1 y label = C2 a las dos fronteras, respectivamente.


// Definicion de la frontera del dominio
int C1 = 1, C2 = 2;
border Gamma1(t= 0, pi){x = cos(t); y = 2*sin(t); label = C1; };
border Gamma2(t= pi, 2*pi){x = cos(t); y = sin(t); label = C2; };

Construcción del mallado

mesh $\Gamma_1$ $\Gamma_2$ .


// Construccion de la triangulacion
mesh Th;
Th = buildmesh( Gamma1(50) + Gamma2(30));
plot(Th, wait = 1);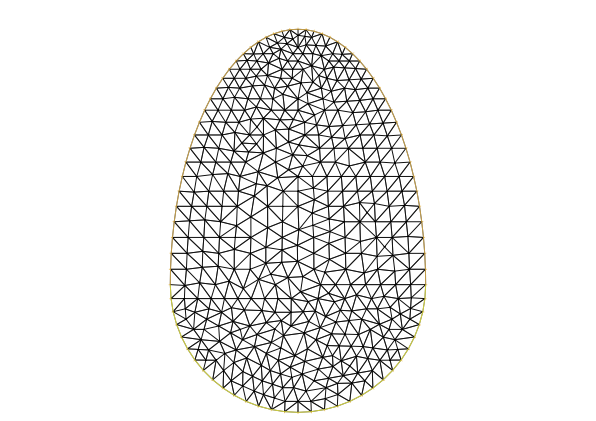

Definición del espacio de elementos finitos

$\mathcal{T}_h$ $W_h$ $\overline{\Omega}$ $T\in\mathcal{T}_h$ es un polinomio de grado menor o igual que 1.


// Definicion del espacio de EF
fespace Wh(Th, P1);

Resolución automática : `solve`

Se va a usar aquí el tipo solve que es muy similar a problem, que ya hemos usado en otros ejemplos, con la diferencia de que define el problema y lo resuelve automáticamente.

$u_0(x,y) \equiv 0$ $g(x,y) \equiv 10$ .

Definimos primero la función del segundo miembro y declaramos las variables del problema.

Se recuerda que en la definición del problema variacional con FreeFEM la ecuación se escribe en forma homogénea (segundo miembro = 0).


// Definicion de la funcion del segundo miembro
func f = 1;

// Declaracion de las variables del problema (elementos de Wh)
Wh u, v;

// Condicion de contorno de Dirichlet homogena y de Neumann no homogenea
func g = 10;
solve Membrana(u, v) = 
    int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v))
  - int2d(Th)( f*v ) 
  - int1d(Th, C2)(g*v)
  + on(C1, u = 0);

// Representacion de la solucion
plot(u, nbiso = 40, cmm ="Condicion de Neumann NO homogenea du/dn = 10", wait = 1);

Aquí, int1d es la función de FreeFEM que sirve para calcular integrales de línea, en este caso sobre la parte de frontera con etiqueta ilabel.

int1d(Th, ilabel)( expresion )

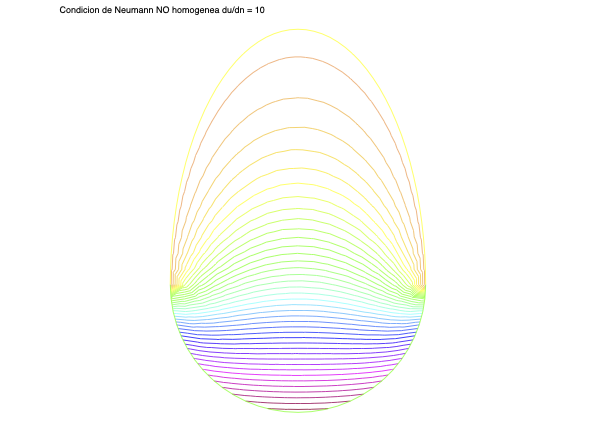
Código completo del programa


// Definicion de la forntera del dominio
int C1 = 1, C2 = 2;
border Gamma1(t= 0, pi){x = cos(t); y = 2*sin(t); label = C1; };
border Gamma2(t= pi, 2*pi){x = cos(t); y = sin(t); label = C2; };

// Triangulacion
mesh Th;
Th = buildmesh( Gamma1(50) + Gamma2(30));

// Definicion de la funcion del segundo miembro
func f = 1;

// Definicion de la condicion de contorno
func g = 10;

// Espacio de elementos finitos
fespace Wh(Th, P1);
Wh u, v;

// Resolucion automatica con solve
solve Membrana(u, v) = 
    int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v))
  - int2d(Th)( f*v ) 
  - int1d(Th, C2)(g*v)
  + on(C1, u = 0);

// Representacion grafica
plot(u, nbiso = 40, cmm="Condicion de Neumann NO homogenea du/dn = 10", wait = 1);

Resolución manual: `varf`

Vamos a considerar ahora otra manera de definir y resolver el problema variacional: usando el tipo varf , construyendo "a mano" la matriz y el segundo miembro y resolviendo el sistema lineal resultante.

Para la formulación del problema variacional, comenzaremos por definir la forma bilineal y la forma lineal asociadas. En este caso:

\begin{matrix} \begin{array}{l} a (u_{h}, v_{h}) = \int_{Ω} (\partial_{x} u_{h} \partial_{x} v_{h} + \partial_{y} u_{h} \partial_{y} v_{h}) d x d y, \\ ℓ (v_{h}) = \int_{Ω} f v_{h} d x d y + \int_{Γ_{2}} g v_{h} d σ . \end{array} \end{matrix}

$\eqref{pb.membrana1.PVh}$ se puede escribir

\begin{matrix} {\begin{cases} Hallar u_{h} \in {\tilde{u}}_{0 h} + V_{h} tal que \\ a (u_{h}, v_{h}) = ℓ (v_{h}) \forall v_{h} \in V_{h} . \end{cases} \end{matrix}

$f(x,y)\equiv 1$ $u_0(x,y) = |x|$ $g(x,y)\equiv 0$ $\Gamma_2$ .

Para definir las formas bilineal y lineal se usa el tipo varf

varf a(u,v) = expresion(u, v)

donde, por convenio, la primera variable, u , es la incógnita y la segunda, v , es la función test. Si en expresion(u,v) no aparece la variable u , se entiende que se está definiendo una forma lineal.

$a(u,v)$ $\ell(v)%$ hay que incluir, además, las condiciones del bloqueo.


xxxxxxxxxx
// Datos del problema:  f y u_0
func f = 1;
func u0 = abs(x);

// Declaracion de las variables del problema (elementos de Wh)
Wh u, v;

// Definicion de la forma bilineal
varf a(u,v) = int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v))
              + on(C1, u = u0);

// Definicion de la forma lineal
varf l(unused, v) = int2d(Th)( f*v ) 
              + on(C1, unused = u0);

Construimos ahora la matriz del sistema, definiéndola como la matriz asociada a la forma bilineal a(u,v) :

\begin{matrix} (1) & A = (a_{i j})_{i, j = 1}^{M}, dada por a_{i j} = a (φ_{i}, φ_{j}) \end{matrix}

$\varphi_i$ $W_h$ . Esta matriz se construye con el tipo matrix , que genera matrices huecas con almacenamiento sparse y contiene ya la penalización debida al bloqueo.


// Matriz asociada a la forma bilineal
matrix A = a(Wh, Wh);

$\eqref{pb.membrana1.PVh}$ $W_h$ .

$w$ $W_h$ ${\cal T}_h$ . Este vector se denota w[]w[][i] $w$ $W_h$ $a_i$ .

Para generar el vector asociado a la forma lineal l(v) antes definida, hay que poner por convenio l(0, Wh) . Internamente, esto hará que no se tenga en cuenta la variable u .


// Segundo miembro
Wh F;
F[] = l(0, Wh); // F[] es el vector asociado al elemento F de Wh

A continuación, resolvemos el sistema lineal resultante. Para ello se utiliza el operador ^-1 que "simboliza" la matriz inversa, de manera que A^-1*bb $A^{-1}b$ $Ax=b$ (piénsese en el operador de MATLAB \ de división matricial por la izquierda). Téngase en cuenta que A^-1 no es en realidad la inversa de A , no genera una matriz.


xxxxxxxxxx
// Resolucion del sistema lineal
u[] = A^-1 * F[]; // u[] es el vector asociado al elemento u  de  Wh

Por último, representamos gráficamente la solución obtenida.


xxxxxxxxxx
// Representacion de la sulucion
plot(u, nbiso = 40, cmm = "Condicion de Neumann homogenea du/dn = 0", wait = 1);

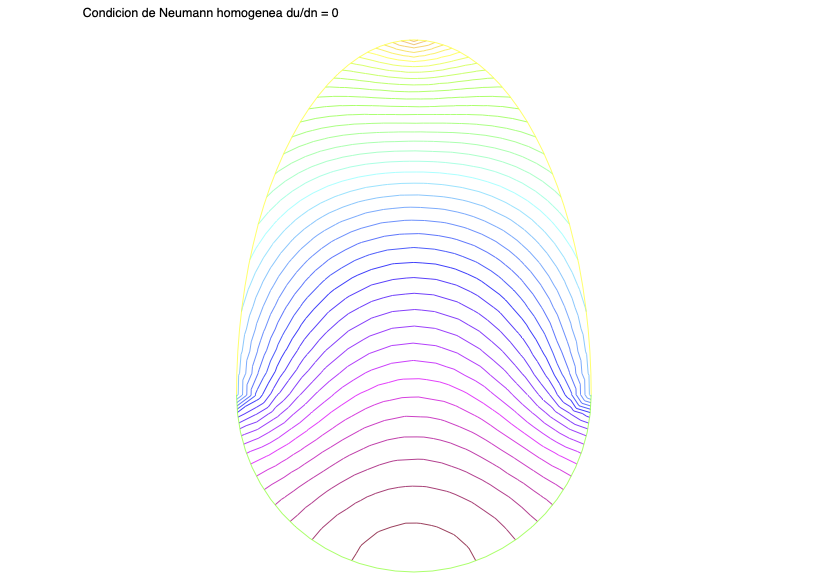
Ejercicio

$\eqref{eq.membrana1}$ $u_0(x,y) \equiv 0$ $g(x,y) \equiv 10$ , realizando la resolución manual con varf.

Código completo del programa


xxxxxxxxxx
int C1 = 98, C2 = 99;
border Gamma1(t= 0, pi){x = cos(t); y = 2*sin(t); label = C1; };
border Gamma2(t= pi, 2*pi){x = cos(t); y = sin(t); label = C2; };

// Triangulacion
mesh Th;
Th = buildmesh( Gamma1(50) + Gamma2(30));
plot(Th, wait = 1);

//  Datos del problema
func f = 1;
func u0 = abs(x);

// Espacio de elementos finitos
fespace Wh(Th, P1);

// Declaracion de las variables del problema
Wh u, v;

// Definicion de la forma bilineal
varf a(u,v) = int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v))
              + on(C1, u = u0);

// Definicion de la forma lineal
varf l(unused, v) = int2d(Th)( f*v ) 
              + on(C1, unused = u0);

// Matriz asociada a la forma bilineal
matrix A = a(Wh, Wh);

// Segundo miembro
Wh F;
F[] = l(0, Wh); // F[] es el vector asociado al elemento F de Wh

// Resolucion del sistema lineal
u[] = A^-1 * F[]; // u[] es el vector asociado al elemento u  de  Wh

// Representacion de la sulucion
plot(u, nbiso = 40, cmm = "Condicion de Neumann homogenea du/dn = 0", wait = 1);

Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla

Ecuación de Poisson con condiciones mixtas Dirichlet-Neumann

Problema considerado

Formulación variacional

Problema aproximado

Resolución con FreeFEM

Definición de la frontera del dominio

Construcción del mallado

Definición del espacio de elementos finitos

Resolución automática : solve

Código completo del programa

Resolución manual: varf

Ejercicio

Código completo del programa

Resolución automática : `solve`

Resolución manual: `varf`