Ecuación de Poisson en un anillo con condiciones de Dirichlet

Resumen: Se resuelve la ecuación de Poisson en un dominio con una cavidad con condiciones de contorno de tipo Dirichlet sobre las dos fronteras.

Problema considerado

$\Omega\subset \mathbb{R}^2$ $\partial \Omega = \Gamma_1\cup \Gamma_2$ $f\in L^2(\Omega)$ $g \in L^2(\Gamma_2)$ $u:\Omega \to \mathbb{R}$ tal que

\begin{matrix} (P) & {\begin{cases} - Δ u = f & en Ω, \\ u = 0 & sobre Γ_{1}, \\ u = g & sobre Γ_{2} . \end{cases} \end{matrix}

Formulación variacional

Observación: todos los cálculos que se hacen en esta sección son puramente formales, es decir, se supone siempre la regularidad suficiente para que todos ellos estén justificados.

$\eqref{eq.poisson2}$ $\widetilde{g}+H_0^1(\Omega)$ $\widetilde{g}\in H^1(\Omega)$ $\widetilde{g}|_{\Gamma_1} = 0$ $\widetilde{g}|_{\Gamma_2} = g$ .

$\eqref{eq.poisson2}$ $v\in H_0^1(\Omega)$ $\Omega$ $v$ $\partial\Omega$ , se obtiene:

\begin{matrix} \int_{Ω} \nabla u \cdot \nabla v d x d y = \int_{Ω} f v d x d y \forall v \in H_{0}^{1} (Ω) . \end{matrix}

$\eqref{eq.poisson2}$ es, por tanto,

\begin{matrix} (PV) & {\begin{cases} Hallar u \in \tilde{g} + H_{0}^{1} (Ω) tal que \\ \int_{Ω} \nabla u \cdot \nabla v d x d y = \int_{Ω} f v d x d y \forall v \in H_{0}^{1} (Ω), \end{cases} \end{matrix}

$\nabla u \cdot \nabla v$ ,

\begin{matrix} {\begin{cases} Hallar u \in \tilde{g} + H_{0}^{1} (Ω) tal que \\ \int_{Ω} (\partial_{x} u \partial_{x} v + \partial_{y} u \partial_{y} v) d x d y = \int_{Ω} f v d x d y \forall v \in H_{0}^{1} (Ω) . \end{cases} \end{matrix}

Problema aproximado

$P_1$ $\partial\Omega$ $\mathcal{T}_h$ $\Omega$ . Consideramos

\begin{matrix} W_{h} = {v_{h} | v_{h} \in C^{0} (\overset{―}{Ω}), v_{h} |_{T} \in P_{1} (T) \forall T \in T_{h}} \subset H^{1} (Ω) \end{matrix}

$\text{dim}\, W_h = M$ $M$ $\mathcal{T}_h$ . Consideramos también

\begin{matrix} V_{h} = {v_{h} | v_{h} \in W_{h}, v_{h} |_{\partial Ω} = 0} \subset H_{0}^{1} (Ω), \end{matrix}

$\mathcal{T}_h$ no $\partial\Omega$ $\eqref{eq.poisson2.var}$ es

\begin{matrix} (PV_{h}) & {\begin{cases} Hallar u_{h} \in {\tilde{g}}_{h} + V_{h} tal que \\ \int_{Ω} (\partial_{x} u_{h} \partial_{x} v_{h} + \partial_{y} u_{h} \partial_{y} v_{h}) d x d y = \int_{Ω} f v_{h} d x d y \forall v_{h} \in V_{h}, \end{cases} \end{matrix}

$\widetilde{g}_h\in W_h$ $\widetilde{g}_h(a_i)= \widetilde{g}(a_i)$ $a_i\in \partial\Omega$ $\Omega$ .

Resolución con FreeFEM

$\Omega$ $(0,1)$ $\partial\Omega = \Gamma_1\cup \Gamma_2$ , viene definida por las curvas

\begin{matrix} \begin{array}{l} Γ_{1} = {(x, y) : x = 2 \cos (t), y = 2 \sin (t), 0 \leq t \leq 2 π}, \\ Γ_{2} = {(x, y) : x = 0.5 \cos (t), y = 1 + 0.5 \sin (t), 0 \leq t \leq 2 π} . \end{array} \end{matrix}

$f(x,y) = xy$ $g(x,y)\equiv 1$ .

Definición de la frontera del dominio

Las siguientes instrucciones definen la frontera del dominio, utilizando sus ecuaciones paramétricas y la dibujan. Obsérvese que hemos asignado la etiqueta 1 a la circunferencia exterior y la etiqueta 2 a la interior usando el comando label .


// Definicion de la frontera del dominio
real R = 2, r = 0.5;
border Gamma1(t = 0, 2*pi){x = R*cos(t); y = R*sin(t);  label = 1;};
border Gamma2(t = 0, 2*pi){x = r*cos(t); y = 1 + r*sin(t); label = 2;};

Construcción del mallado

mesh $\Gamma_1$ $\Gamma_2$ $\Gamma_2$ recorre la curva en el sentido contrario, debemos indicar (convenio de FreeFEM) un número negativo de segmentos sobre dicha frontera.


xxxxxxxxxx
// Construccion de la triangulacion
mesh Th = buildmesh(Gamma1(60)+ Gamma2(-40));
plot(Th, cmm = "Triangulacion", wait = 1);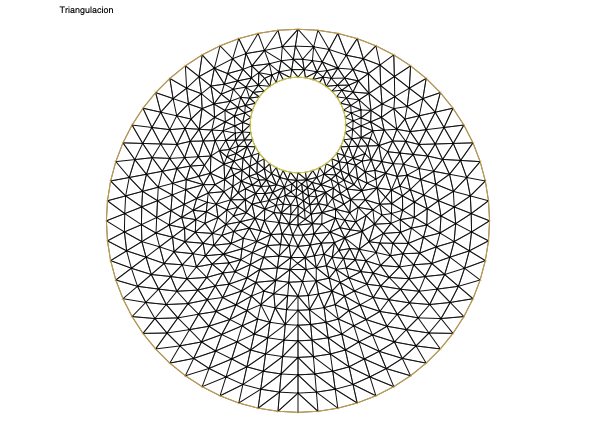

Definición del espacio de elementos finitos

$\mathcal{T}_h$ $W_h$ $\overline{\Omega}$ $T\in\mathcal{T}_h$ es un polinomio de grado menor o igual que 1.


// Definicion del espacio de EF
fespace Wh(Th, P1);

Definición del problema variacional

$u=0$ $\Gamma_1$ $u=g$ $\Gamma_2$ bloqueo $\eqref{poisson2.pvh}$ $W_h$ .

Se recuerda, también, que en la definición del problema variacional con FreeFEM la ecuación variacional se escribe en forma homogénea (segundo miembro = 0).


// Definicion de la funcion del segundo miembro
func f = x*y;

// Declaracion de las variables del problema (elementos de Wh)
Wh u, v;

// Definicion del problema variacional; lo denotamos MiPoisson
problem MiPoisson(u, v) = 
        int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v)) 
      - int2d(Th)( f*v )
      + on(1, u = 0)
      + on(2, u = 1);

Resolución del problema y representación


// Resolucion
MiPoisson;

// Dibujo de la solucion
plot(u, nbiso = 50, value = true, wait = 1,
      cmm =" Pulsa 3 para alternar entre 2d y 3d; pulsa f para ver rellenos");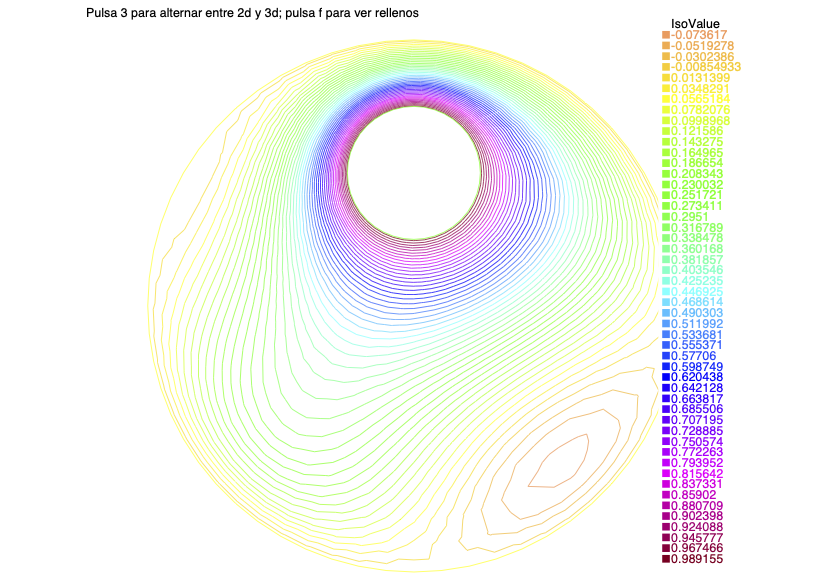

Ejercicios

Se proponen los siguientes ejercicios como variantes del problema:

$P_2$ $P_1$ , usando una triangulación grosera.
Usar mallados mas y menos finos.

Código completo del programa


// Definicion de la frontera del dominio
real R = 2, r = 0.5;
border Gamma1(t = 0, 2*pi){x = R*cos(t); y = R*sin(t);label = 1;};
border Gamma2(t = 0, 2*pi){x = r*cos(t); y = 1 + r*sin(t); label = 2;};

// Construccion de la triangulacion
mesh Th;
Th = buildmesh(Gamma1(60)+ Gamma2(-40));
plot(Th, cmm = "Triangulacion", wait = 1);

// Definicion del espacio de elementos finitos 
fespace Wh(Th, P1);

// Definicion de la funcion del segundo miembro
func f = x*y;

// Declaracion de las variables del problema 
Wh u, v;

// Definicion del problema variacional
problem MiPoisson(u, v) = 
        int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v)) 
    - int2d(Th)( f*v )
    + on(1, u = 0)
    + on(2, u = 1);

// Resolucion 
MiPoisson;

// Dibujo de la solucion
plot(u, nbiso = 50, value = true, wait = 1,
      cmm =" Pulsa 3 para alternar entre 2d y 3d; pulsa f para ver rellenos");

Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla