Stokes2D.edp
Resumen: En este ejemplo se considera el problema estacionario de Stokes bidimensional.
Problema considerado
Sea
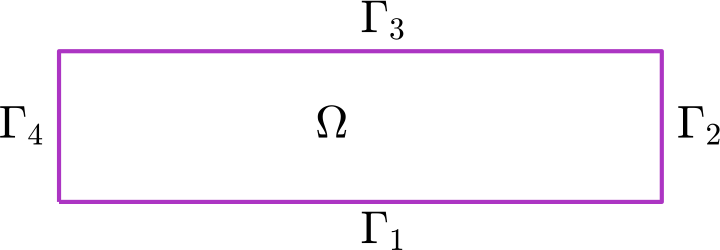
Denotamos
donde
Formulación débil
Sea
donde
La formulación
Se observa que la forma bilineal que aparece en
Se considera entonces una regularización del problema
Este problema regularizado posee solución única, puesto que ahora sí se verifican las hipótesis del Teorema de Lax-Milgram.
Problema aproximado
Vamos a utilizar una aproximación mediante elementos finitos
y
El problema aproximado de
Resolución con FreeFEM
Resolvemos el problema para
Código
x//// Data://real xnu = 1., f1 = 1.,f2 = 0.;real Uh = 1.e5;real epsr = 1.e-8;
//// Mesh://mesh Th = square(10,10,flags=3); plot(Th,wait = 1);
//// Finite element space// [u1, u2, p] : unknown// [v1, v2, p] : function test//fespace Vh(Th,P2); fespace Ph(Th,P1);
Vh u1,u2,v1,v2;Ph p,q;
//// Macro definitions:// Macros can have arguments (like those ones) and MUST finish by //macro Grad(u,v) [dx(u), dy(v), dx(v), dy(u)] // macro div(u1,u2) (dx(u1)+dy(u2)) //
//// Problem + Solution:// solve Stokes( [u1,u2,p],[v1,v2,q] ) = int2d(Th) ( xnu*Grad(u1,u2)'*Grad(v1,v2) - p*div(v1,v2) + div(u1,u2)*q + epsr*p*q ) + on(1,2,4, u1 = 0.,u2 = 0.) + on(3, u1 = Uh,u2 = 0.); //// Plots//plot([u1,u2],wait = true,value = true);plot(p,wait = true,value = true ,fill = true ,nbiso = 40);
Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla