Ecuación de ondas acoplada con ec. parabólica
Resumen: En este ejemplo se considera un problema relativo a la ecuación de ondas, en la aparece una función que, a su vez, es solución de una ecuación parabólica.
Problema considerado
Sean
donde
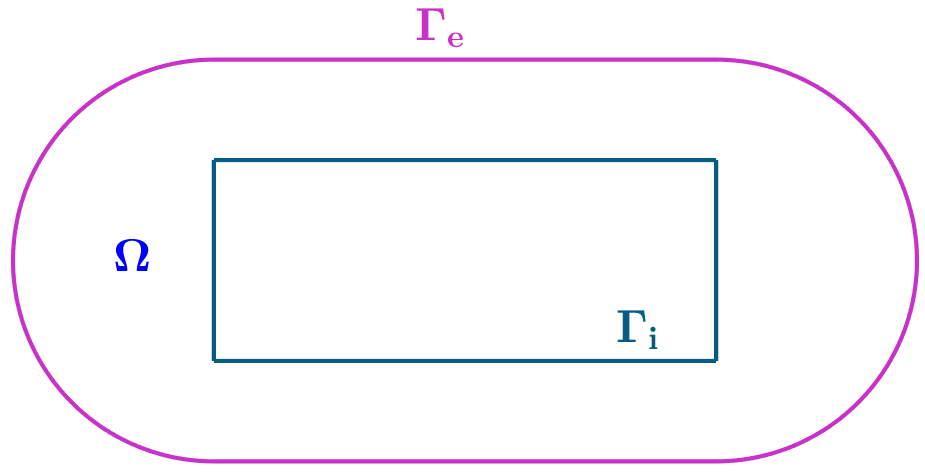
Lo primero que hacemos notar es que, en
y, a continuación, calcular
Procediendo como en ejemplos anteriores, en los problemas
Discretización en tiempo
Consideramos una partición uniforme del intervalo
Denotamos
Se obtienen así las dos sucesiones siguientes de problemas
Problemas estacionarios para
- Tomar
- Para cada
Problemas estacionarios para
- Tomar
- Para cada
Formulación débil o variacional
La formulación variacional de los problemas
donde
Obsérvese que todos los problemas
y que solo difieren en la forma lineal. En la resolución numérica, esto se traduce en el hecho de que todos los sistemas lineales a resolver tienen la misma matriz, que, por lo tanto, solo habrá que construir y factorizar la primera vez.
La formulación variacional de los problemas
Código
x
// TempWave2D.edp (version 1)//// P2 spatial finite elements// Implicit Euler for time discretization//// Solutions of stationnary problems are computed and saved // in an FE functions array and plotted in two different windows at the end// At the beginning of the plots, arrange windows in order to see both of them//
//// Data//real T=8.; // Final timereal x1=0., x2=5., y1=0., y2=4., z1=1., z2=3.; // Domain geometryreal a = 1.e-2, b = 1., c = 5.; // PDE coefficients
func f = 1.; // ffunc gE = 1.; // g_efunc gI = 0.; // g_ifunc u0 = y*(1.-y)*(y-3.)*(4.-y); // u_0//func u0=y*(4.-y);func w0 = 50.*sin(pi*y/4.); // w_0func w1 = 0.; // w_1
int nt = 200;int nu = 3; // number of segment discretization per unit of length
//// Coefficients of stationnary problems//real dt = T/nt;real dt1 = 1./dt;real dt2 = dt1^2;real dt22 = 2*dt2;real c2 = c*c;
//// Border//// outer boundaryint LE=9, LI=12; // Labelsreal pi2 = pi/2., pi23 = 3.*pi2;real R = (y2-y1)/2., ymed = (y1+y2)/2.; // radius and center of semicirc.border CE1(t = 0., 1.){ x = x1 + t*(x2-x1); y = y1; label = LE;}border CE2(t = -pi2, pi2){x = x2 + R*cos(t); y = ymed + R*sin(t); label = LE;}border CE3(t = 0., 1.){ x = x2 - t*(x2-x1); y = y2 ; label = LE;}border CE4(t = pi2, pi23){x = x1 + R*cos(t); y = ymed + R*sin(t); label = LE;}// inner boundaryborder CI1(t = 0., 1.){x = x2-t*(x2-x1); y = z1; label = LI;}border CI2(t = 0., 1.){x = x1; y = z1+t*(z2-z1); label = LI;}border CI3(t = 0., 1.){x = x1+t*(x2-x1); y = z2; label = LI;}border CI4(t = 0., 1.){x = x2; y = z2-t*(z2-z1); label = LI;}
//// Mesh//mesh Th = buildmesh(CE1(5*nu)+CE2(6*nu)+CE3(5*nu)+CE4(6*nu) +CI1(5*nu)+CI2(2*nu)+CI3(5*nu)+CI4(2*nu)); //// FE space//fespace Vh(Th,P2);Vh u, w, v;Vh fh = f;Vh uold; // uold --> u^{i-1}Vh wold1, wold2; // wold1 --> w^{i-1}, wold2 --> w^{i-2}Vh F; // RHS to be defined at each iterationVh gEh = gE, gIh = gI;
//// Stationnary problems//
// Heat PDEproblem Heat(u, v, init = 1) = int2d(Th)(dt1*u*v + a*(dx(u)*dx(v) + dy(u)*dy(v))) - int2d(Th)(F*v) + on(LE, u = gEh) + on(LI, u = gIh);
// Wave PDEproblem Wave(w, v, init = 1) = int2d(Th)(dt2*w*v + c2*(dx(w)*dx(v) + dy(w)*dy(v))) - int2d(Th)(F*v) + on(LI, w = 0.);
//// Computations//// Initializations//int nt1 = nt+1;Vh[int] U(nt1), W(nt1);
// Two first steps for uU[0] = u0;uold = u0;F = fh + dt1*uold;Heat;U[1] = u;
// Two first steps for wwold1 = w0;w = w0 + dt*w1;W[0] = wold1;W[1] = w;
//// Time iterates// for (int k= 2; k <= nt; k++){ uold = u; F = fh + dt1*uold; Heat; wold2 = wold1; wold1 = w; F = b*u + dt22*wold1 - dt2*wold2; Wave; U[k] = u; W[k] = w;}
//// Plots//real t;plot(U[nt], dim = 3, WindowIndex=0);plot(W[0], dim = 3, WindowIndex=1);for (int k = 0; k <= nt; k++){ t = k*dt; plot(U[k], WindowIndex=0, dim = 3, fill = true, nbiso = 40, value=true, prev=true, cmm = "Heat. Time = " + t, wait = true); plot(W[k], WindowIndex=1, dim = 3, fill = true, nbiso = 40, value=true, prev=true, cmm = "Wave. Time = " + t, wait = true);}
Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla