Transferencia del calor
Resumen: En este ejemplo vamos a considerar la ecuación del calor estacionaria escrita en forma de divergencia con un coeficiente de difusión no constante y definido a trozos. Veremos también cómo exportar la triangulación a un archivo externo.
Problema considerado
Sea
donde
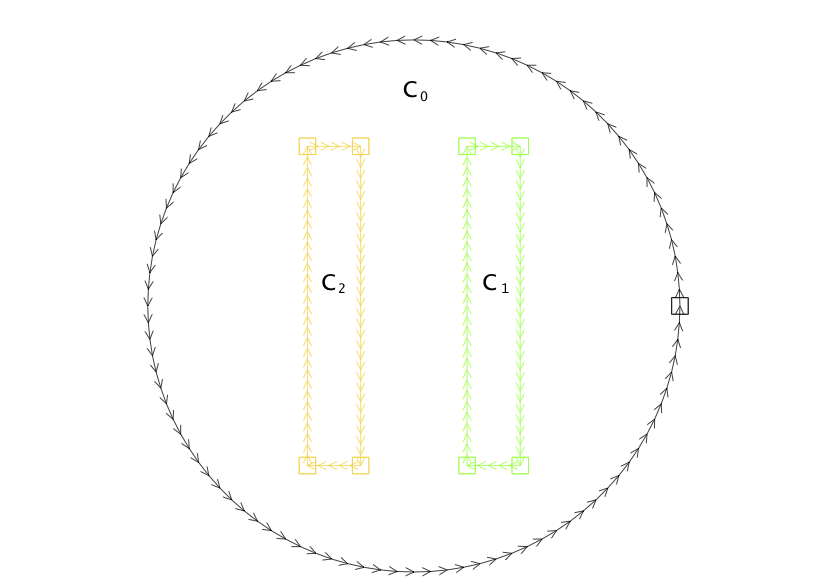
Este problema modela, por ejemplo, el estado estacionario de un sistema formado por dos conductores térmicos rectangulares que se encuentran dentro de un recinto circular. Uno de los conductores (
Formulación variacional
Observación: todos los cálculos que se hacen en esta sección son puramente formales, es decir, se supone siempre la regularidad suficiente para que todos ellos estén justificados.
El espacio natural para buscar la solución del problema
Para obtener la formulación variacional de
La formulación variacional de
Problema aproximado
Vamos a utilizar una aproximación mediante elementos finitos
con
cuya dimensión es igual al número de vértices de
donde
Resolución con FreeFEM
Tomaremos como
Definición de la frontera del dominio
Cada uno de los bordes de los rectángulos label = 6 al borde del rectángulo label = 2 al del rectángulo label = 90 a la circunferencia exterior
// Datosreal xa = 1., yb = 3.;real r = 5.;int CC0 = 90, CC1 = 6, CC2 = 2;
// Definicion del borde// Frontera exterior del dominioborder C0(t = 0, 2*pi){x = r*cos(t); y = r*sin(t); label = CC0;};// Rectangulo C1 border C11(t=0., 1.){x = xa+t; y = yb; label = CC1;};border C12(t=0., 1.){x = xa+1; y = yb*(1-2*t); label = CC1;};border C13(t=0., 1.){x = xa-t+1; y = -yb; label = CC1;};border C14(t=0., 1.){x = xa; y = yb*(2*t-1); label = CC1;};// Rectangulo C2 border C21(t=0., 1.){x = -xa-(1-t); y = yb; label = CC2;};border C22(t=0., 1.){x = -xa; y = yb*(1-2*t); label = CC2;};border C23(t=0., 1.){x = -xa-t; y = -yb; label = CC2;};border C24(t=0., 1.){x = -xa-1; y = yb*(2*t-1); label = CC2;};Construcción del mallado
Declaramos primero una variable tipo mesh y después construimos una triangulación del dominio. Se observa que el interior del rectángulo
// Construccion de la triangulacionmesh Th;Th = buildmesh( C0(100) + C11(5) + C12(30) + C13(5) + C14(30) + C21(-5) + C22(-30) + C23(-5) + C24(-30) );plot( Th , wait = 1);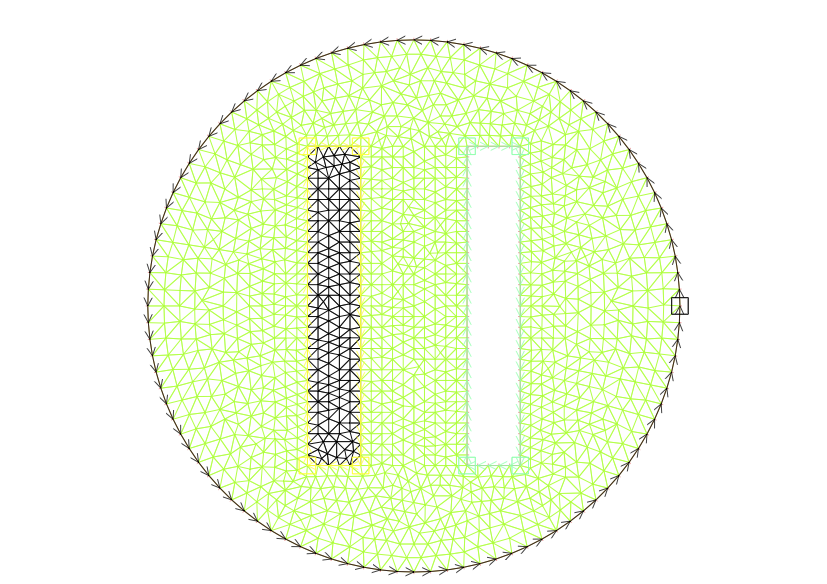
Definición del espacio de elementos finitos
Definimos el espacio de elementos finitos que vamos a utilizar sobre
// Definicion del espacio de EFfespace Wh(Th, P1);Definición del problema variacional
Se recuerda que las condiciones de Dirichlet (en este caso
// Declaracion de las variables del problema (elementos de Wh)Wh u, v;Además, tenemos que definir el coeficiente W0 de funciones que son constantes por triángulos, declaramos que
// Definicion del coeficiente kappa// kappa = 1 en Omega \setminus C2// kappa = 3 en C2fespace W0(Th, P0);W0 kappa = 1 + 2*(x<-1)*(x>-2)*(y<3)*(y>-3);plot(kappa, wait = 1, fill = true, ps = "kappa.eps");
Definimos de forma habitual el problema variacional usando el tipo problem
// Definicion del problema variacionalproblem HeatEx(u, v) = int2d(Th)(kappa*(dx(u)*dx(v)+dy(u)*dy(v))) + on(CC0, u = 20) + on(CC1, u = 60);Resolución del problema y representación
// ResolucionHeatEx;
plot(u, C0(100) + C11(5) + C12(30) + C13(5) + C14(30) + C21(-5) + C22(-30) + C23(-5) + C24(-30), wait = 1);
// Dibujo de la solucionplot(u, wait = 1);
Código completo del programa
// Datosreal xa = 1., yb = 3.;real r = 5.;int CC0 = 90, CC1 = 6, CC2 = 2;
real[int] colorhsv=[ // modelo de color hsv 0.6, 0.9, 1.0,1.0, 0.9, 1.0 ];
// Definicion del borde// Circunferencia C0border C0(t = 0, 2*pi){x = r*cos(t); y = r*sin(t); label = CC0;};// Rectangulo C1 border C11(t=0., 1.){x = xa+t; y = yb; label = CC1;};border C12(t=0., 1.){x = xa+1; y = yb*(1-2*t); label = CC1;};border C13(t=0., 1.){x = xa-t+1; y = -yb; label = CC1;};border C14(t=0., 1.){x = xa; y = yb*(2*t-1); label = CC1;};// Rectangulo C2 border C21(t=0., 1.){x = -xa-(1-t); y = yb; label = CC2;};border C22(t=0., 1.){x = -xa; y = yb*(1-2*t); label = CC2;};border C23(t=0., 1.){x = -xa-t; y = -yb; label = CC2;};border C24(t=0., 1.){x = -xa-1; y = yb*(2*t-1); label = CC2;};
// Triangulacionmesh Th;Th = buildmesh(C0(100) + C11(5) + C12(30) + C13(5) + C14(30) + C21(-5) + C22(-30) + C23(-5) + C24(-30) );plot(Th, C0(100) + C11(5) + C12(30) + C13(5) + C14(30) + C21(-5) + C22(-30) + C23(-5) + C24(-30), wait = 1);
// Espacio de elementos finitos: P1fespace Wh(Th, P1);Wh u, v;
// Definicion del coeficiente kappa// kappa = 1 en Omega \setminus C2// kappa = 3 en C2fespace W0(Th, P0);W0 kappa = 1 + 2*(x<-1)*(x>-2)*(y<3)*(y>-3);plot(kappa, wait = 1, fill = true, ps = "kappa.eps");
// Definicion del problemaproblem HeatEx(u, v) = int2d(Th)(kappa*(dx(u)*dx(v)+dy(u)*dy(v))) + on(CC0, u = 20) + on(CC1, u = 60);
// ResolucionHeatEx;
// Representacionplot(u, wait = 1, fill = true, hsv = colorhsv);
Complementos
Se puede salvar la triangulación para usarla en otro programa usando el comando savemesh. Se guardan los números de las etiquetas de las fronteras, pero no se guardan los nombres de las variables que hemos usado para definirlas (en este ejemplo CC0 , CC1 y CC2). Para usarlas posteriormente, hay que utilizar expresamente sus valores.
savemesh(Th, "triangulacion.msh");Más concretamente, para resolver el problema de este ejemplo, una vez guardada la triangulación en un fichero, hay que leerla usando el comando readmesh y la resolución del problema se haría de la forma siguiente:
// Lectura de la triangulacionmesh Th = readmesh("triangulacion.msh");
// Espacio de elementos finitos: P1fespace Vh(Th, P1);Vh u, v;
// Definicion del coeficiente kappa// kappa = 1 en Omega \setminus C2// kappa = 3 en C2fespace W0(Th, P0);W0 kappa = 1 + 2*(x<-1)*(x>-2)*(y<3)*(y>-3);
// Definicion del problemaproblem HeatEx(u, v) = int2d(Th)(kappa*(dx(u)*dx(v)+dy(u)*dy(v))) + on(90, u = 20) + on(6, u = 60); // Resolucion y representacion graficaHeatEx;plot(u, wait = 1);
Ejercicio
Resolver el problema varf.
Anna Doubova - Rosa Echevarría - Dpto. EDAN - Universidad de Sevilla